Portfólio: O gato de Schrörzenegger: mudanças entre as edições
| (21 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 35: | Linha 35: | ||
No caso da velocidade média podemos ter como a razão entre o deslocamento (ΔS), do corpo e o intervalo de tempo (Δt), durante o qual esse deslocamento ocorreu. Sendo expressa da seguinte forma: | No caso da velocidade média podemos ter como a razão entre o deslocamento (ΔS), do corpo e o intervalo de tempo (Δt), durante o qual esse deslocamento ocorreu. Sendo expressa da seguinte forma: | ||
<math>v_m | <math>v_m = \frac{\Delta S}{\Delta t} = \frac{S-S0}{t-t0}</math> | ||
Pela notação temos que s0 é a posição ocupada pelo corpo no instante t1, e S no instante t. A unidade da velocidade média que se faz uso no SI é o metro por segundo (m/s). | Pela notação temos que s0 é a posição ocupada pelo corpo no instante t1, e S no instante t. A unidade da velocidade média que se faz uso no SI é o metro por segundo (m/s). | ||
| Linha 41: | Linha 42: | ||
Sendo expressa da seguinte forma: | Sendo expressa da seguinte forma: | ||
<math>v_i | <math>v_i = \lim_{\Delta t\to\ 0}\frac{\Delta S}{\Delta t} = \frac{dx}{dt}</math> | ||
Pela notação, observe que v, é a taxa com a qual a posição S, está variando com o tempo em um dado instante, isto é, v é a derivada de S em relação a t. A unidade utilizada é (m/s). | Pela notação, observe que v, é a taxa com a qual a posição S, está variando com o tempo em um dado instante, isto é, v é a derivada de S em relação a t. A unidade utilizada é (m/s). | ||
| Linha 268: | Linha 269: | ||
=====Resultados==== | =====Resultados===== | ||
Px= P . | Px = P . sen35° => Px = m . g . sen35° | ||
Py = P . cos35° => Py = n . g . cos35° | |||
N = Py => N = m . g . cos35º | |||
Fat = Px => Fat= m . g . sen35° | |||
Fatmáx = μe . N | |||
μe = <math>\frac{Fatmáx}{N}</math> => μe = <math>\frac{ m . g . sen35°}{m . g . cos35°}</math> => μe = <math>\frac{sen35°}{cos35°}</math>= 0,70. | |||
N = m . g . cos35° | |||
N = 0,08418 . 10 . cos35° | |||
N = 0,69N | |||
Fatmáx = μe . N | |||
Fatmáx = 0,70 . 0,69 | |||
Fatmáx = 0,483N | |||
===Conclusão=== | ===Conclusão=== | ||
==Programação Scratch== | |||
===Poligonos=== | |||
Clique nos Links para ver os arquivos funcionando e explora-los mais a fundo. | |||
'''1-''' Aprimorar o programa para desenhar polígonos regulares, permitindo que o usuário escolha quantos lados terá o polígono a ser desenhado. | |||
'''2-''' Aprimore o programa incluindo um limite para o número de lados possíveis para o polígono, por exemplo, entre 3 e 12 lados. Use testes com Se/Então/Senão. | |||
'''3-''' Aprimore o programa de forma a diminuir o número de passos do gatinho em função do número de lados do polígono, permitindo que o desenho caiba na área do palco, mesmo para polígonos com mais de 12 lados. | |||
'''R:''' Concluindo as três questões obtemos o seguinte resultado: | |||
*[https://scratch.mit.edu/projects/255635765 Polígonos de quantos lados quiser] | |||
'''4-''' Explique qual seria a lógica para que o gatinho desenhasse um círculo? | |||
'''R:''' para que o gatinho desenhe um círculo, é necessário um numero muito grande de retas muito pequenas, divergindo o ângulo a cada reta, assim, no programa, o mais intuitivo de se fazer é, programar o gatinho para que ele de um passo, e vire 1° grau (sempre para o mesmo lado), repetindo 360 vezes, pois assim ele irá definir um circulo perfeito, concluindo os 360° graus do círculo. O arquivo a seguir contem vários polígonos e por final o gatinho define um círculo contendo todos os polígonos dentro | |||
*[https://scratch.mit.edu/projects/255639723 Polígonos Variados] | |||
===Movimento Retilíneo Uniforme=== | |||
[[Mídia:MRU2.sb| Lançamento vertical no vácuo]] | |||
==Referências== | ==Referências== | ||
Edição atual tal como às 21h25min de 13 de novembro de 2018
- Curso
- Licenciatura em Física
- Disciplina
- Informática Aplicada ao Ensino de Física
- Professor
- Evandro Cantú
- Equipe
- Nicolas
- Christopher
- Lucas
Experimento: Tempo de reação humana
O experimento teve como objetivo medir o tempo de reação humana, utilizando uma régua de 30 cm, a qual foi deixada cair e capturada antes de cair no chão.O tempo de reação foi medido com um cronômetro [1].
--Nicolas.trindade (discussão) 20h08min de 25 de setembro de 2018 (BRT)
--Lucas.santos (discussão) 20h19min de 25 de setembro de 2018 (BRT)
Gráficos com a Planilha de Cálculo
--Christopher.barboza (discussão) 20h15min de 25 de setembro de 2018 (BRT)
Experimento: Velocidade média e Instantânea
introdução
É tido como um dos inúmeros objetivos da física o estudo do movimento dos objetos: a rapidez com que se movem, como exemplo, ou a distância percorrida em um certo intervalo de tempo. (Walker, 2016).
Velocidade média e instantânea
A velocidade é uma grandeza vetorial, deste modo possui um módulo e uma orientação (direção e sentido), e pode também ser representada por componentes. Se um corpo se move de um ponto a outro no espaço, é possível calcular a “rapidez”, com que este corpo se move. Pode-se definir duas grandezas que expressam essas “rapidez” de um movimento: velocidade média e velocidade instantânea. No caso de um movimento bidimensional e tridimensional, deve- se considerar essas grandezas como vetores e utilizar a notação vetorial. (Walker, 2016). No caso da velocidade média podemos ter como a razão entre o deslocamento (ΔS), do corpo e o intervalo de tempo (Δt), durante o qual esse deslocamento ocorreu. Sendo expressa da seguinte forma:
Pela notação temos que s0 é a posição ocupada pelo corpo no instante t1, e S no instante t. A unidade da velocidade média que se faz uso no SI é o metro por segundo (m/s).
Já no caso da velocidade instantânea, ela é obtida a partir da velocidade média reduzindo o intervalo de tempo (Δt) até torná-lo próximo de zero. Quando Δt diminui, a velocidade média se aproxima cada vez mais de um valor limite, que é a velocidade instantânea. (Walker,2016).
Sendo expressa da seguinte forma:
Pela notação, observe que v, é a taxa com a qual a posição S, está variando com o tempo em um dado instante, isto é, v é a derivada de S em relação a t. A unidade utilizada é (m/s).
Objetivos
Os objetivos deste experimento experimental são: analisar o movimento de uma bolinha ao descer a calha e calcular a velocidade média, elaborar um procedimento experimental para estimar a velocidade instantânea.
Materiais e Procedimentos
Na realização do experimento foram utilizadas duas calhas com inclinação estabelecida pelo grupo, uma esfera (bolinha de gude), cronômetro e trena. 1 - Coloque a esfera no topo da calha e deixe rolar. Com um cronômetro, meça o tempo que a esfera gasta para descer a calha com uma inclinação pequena. Anote o resultado.
| Medidas | Tempo Total(s) |
| 1 | 2,90 |
| 2 | 2,95 |
| 3 | 2,81 |
| 4 | 2,80 |
| 5 | 2,92 |
| Média | 2,876 |
O tempo gasto para descer toda a calha foi de 2,876s.
2 - Calcule a partir do tempo medido a velocidade da esfera ao descer a calha usando a expressão: v=
RS: v== 0,379m/s.
3 - A velocidade calculada acima é realmente a velocidade com que a esfera desce a calha ou é apenas a velocidade média? Explique.
RS:Apenas a Velocidade média, pois, a velocidade nos instantes iniciais são muito inferiores às velocidades dos instantes finais. Como há uma inclinação a bolinha tende a acelerar, fazendo com que a bolinha adquira uma velocidade cada vez maior durante o percurso.
4 - Você acha que o tempo que a esfera gastaria para descer a primeira metade da calha é metade do tempo para descer a calha inteira, mais da metade ou menos da metade? Justifique. (Responder antes de realizar a medida).
RS:Não, mais da metade do tempo. Porque, na primeira metade da calha a velocidade inicial é 0, com uma aceleração X. Na segunda metade da calha, a velocidade inicial é igual a velocidade final da primeira metade da calha e com a mesma aceleração X. No entanto a distância na qual a bolinha deve percorrer, na segunda metade da calha, é equivalente à distância da primeira metade, sendo que, a bolinha já contém uma velocidade, mantendo a mesma aceleração, isso faz com que o tempo seja menor.
5 - Meça agora o tempo que a esfera gasta para descer a primeira metade da calha e anote o resultado.
Tabela 2: Tempo de descida 1 e 2
| Medidas | Primeira Metade(s) | Segunda Metade(s) |
| 1 | 1,94 | 0,96 |
| 2 | 1,89 | 1,13 |
| 3 | 1,92 | 0,96 |
| 4 | 2,00 | 0,95 |
| 5 | 1,97 | 0,91 |
| Média | 1,944 | 0,982 |
Tempo gasto para descer a primeira metade da calha foi de 1,94s
6 - Esta medida está de acordo com a sua previsão? Caso não esteja, explique a diferença.
RS:Sim, pois o tempo gasto é maior do que o da segunda metade como previsto.
7 - Calcule a velocidade média na primeira metade da calha e na segunda metade da calha. Compare os resultados com aquele obtido na questão 2.
| Primeira Metade | Segunda Metade |
| s= 0,545m | S= 0,545m |
| t= 1,944 s | T= 0,982 s |
| Vméd= 0,2803 m/s | Vméd= 0,555 m/s |
Tabela 3: Velocidades médias 1 e 2
Na primeira metade da calha, o valor da velocidade é abaixo da velocidade média. Na segunda metade da calha esse valor é acima da velocidade média.
8 - Vamos agora estimar a velocidade instantânea da bolinha quando ela passa por um ponto da calha, e não mais a velocidade média em todo o percurso. Elabore uma maneira de realizar esta estimativa para um ponto situado a 20 cm do início da calha. Descreva em detalhes o procedimento proposto pelo grupo e discuta os resultados obtidos.
RS: O experimento proposto foi, marcar o ponto A: 20 cm do inicio da calha e o ponto B:10 cm do inicio da calha, e medir com ajuda de um cronômetro o tempo que a bolinha levou para percorrer a distância de B até A, resultando em um intervalo de tempo pequeno, assim podemos encontrar um valor aproximado da velocidade instantânea, pois como o tempo irá tender à zero podemos encontrar um valor muito próximo da verdadeiro valor. Então temos:
| Medidas | Intervalo de tempo entre, A e B |
| 1 | 0,48s |
| 2 | 0,47s |
| 3 | 0,35s |
| 4 | 0,39s |
| 5 | 0,35s |
| Média | 0,41s |
Tabela 4: Intervalo de tempo entre B e A
Com isso, e tendo conhecimento que a distância entre os pontos B e A é de 10 cm, utilizamos a fórmula v= St, para obtermos aproximadamente a velocidade instantânea: v== 0,244m/s
9 - Utilizando o mesmo procedimento da questão anterior, para descobrir a velocidade da bolinha no instante em que ela passa por um ponto situado a 20 cm do final da calha. Comparar esse valor com o obtido na questão 7. Vocês esperavam esta diferença?
RS:Nesta nova medida, foi preciso adaptar algumas coisas, marcamos novamente um ponto A, mas desta vez à 20 cm do final da calha, e um ponto B à 50 cm do final da calha, resultando em uma distância entre o ponto B e o ponto A de 30 cm, esta distância foi necessária, pois, estávamos fazendo a medida com cronômetros manuais, então os reflexos humanos entram em ação prejudicando uma medida mais precisa em um intervalo menor de distância e consequentemente, menor em tempo. Com tal construção temos:
| Medidas | Intervalo de tempo entre, A e B |
| 1 | 0,53s |
| 2 | 0,60s |
| 3 | 0,46s |
| 4 | 0,53s |
| 5 | 0,59s |
| Média | 0,542s |
Tabela 5: Intervalo de tempo entre B e A
Com isso, e tendo conhecimento que a distância entre os pontos A e B é de 30 cm, utilizamos a fórmula v= St, para obtermos aproximadamente a velocidade instantânea:
v== 0,555m/s
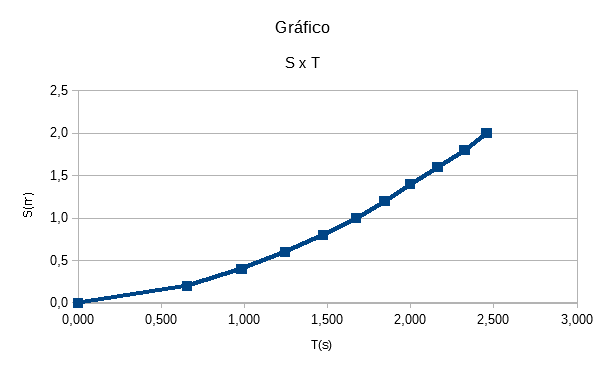
10 - Elabore um procedimento para coletar dados e construir um gráfico da posição versus tempo para o movimento da bolinha. A partir deste gráfico, determine a equação para este movimento.
RS:Primeiramente o grupo utilizou uma segunda calha (com um comprimento maior), pegou-se a calha e colocou sobre uma base (criando uma inclinação). Medindo o comprimento da calha, constatou-se que a mesma possuía 2 metros, desde modo a cada 20 cm era feita uma marcação na calha. Para fazer então a coleta de dados a fim de determinar o gráfico (posição X tempo), fez-se o uso de um celular (para filmar o movimento a ser realizado pela bolinha de gude) e um cronômetro (colocado no mesmo plano da filmagem (a fim de obter a marcação temporal). Com um auxílio de um editor de vídeo foi possível determinar a posição ocupada pela bolinha em determinado instante, conforme mostrado na tabela 6 e no gráfico 1.
| Medidas | Distância (m) | Tempo Obtido (s) |
| 0 | 0,0 | 0,00 |
| 1 | 0,2 | 0,655 |
| 2 | 0,4 | 0,972 |
| 3 | 0,6 | 1,244 |
| 4 | 0,8 | 1,473 |
| 5 | 1,0 | 1,671 |
| 6 | 1,2 | 1,741 |
| 7 | 1,4 | 1,997 |
| 8 | 1,6 | 2,160 |
| 9 | 1,8 | 2,324 |
| 10 | 2,0 | 2,455 |
11- Como vocês analisam a precisão das medidas realizadas neste experimento? Elas são confiáveis? Até que ponto? Quais aspectos são relevantes para esta análise, ou seja, quais fatores poderiam levar a erros nas medidas realizadas? Vocês se contentaram em fazer apenas uma medida em cada experimento ou fez várias medidas para obter dados mais confiáveis?
RS:O grupo realizou o experimento de forma satisfatória, a precisão do mesmo está inteiramente ligada aos materiais usados, não sendo tão exata como poderia ser, se comparado com práticas experimentais com o auxílio de instrumentos mais adequados. As medições remontam a realidade do sistema analisado, para entender o movimento e atestar a confiabilidade do mesmo a ponto de entender seu comportamento, mas não para determinar com exatidão a velocidade instantânea do corpo em um determinado ponto. Tendo em vista obter uma melhor aproximação dos valores apresentados no sistema, avaliando o conjunto de 10 medições de modo a maximizar o processo e minimizar os possíveis erros. Alguns fatores que podem levar a erros nas medidas neste experimento, erro de paralaxe, quando o deslocamento aparente de um objeto muda quando se muda o ponto de observação, imprecisão dos instrumentos utilizados e falhas humanas como, determinação incorreta nas leituras dos tempos.
Conclusão
O concluso relatório, apresentou de modo coeso, um método satisfatório para obtenção de dados na análise de um sistema de deslocamento, o grupo salientou a realização do experimento da forma mais satisfatória dentro de suas limitações, a precisão do experimento está está inteiramente calcada aos materiais alternativos utilizados, se comparado com práticas experimentais com o auxílio de instrumentos mais adequados o experimento pode conter incongruências devido não somente a falta de materiais adequados mas também a falta de experiência do grupo. Tendo em vista obter uma melhor aproximação dos valores apresentados no sistema, avaliando o conjunto de 10 medições de modo a minimizar os possíveis erros, o presente relatório está perfeitamente amparado no que diz respeito à, compreender o movimento e atestar a confiabilidade do mesmo no sistema, à ponto de entender seu comportamento ecumênico.
Experimento II: Determinação do coeficiente de atrito
Introdução
Força de Atrito:
A força de atrito se opõe ao movimento, ela depende da natureza da superfície(coeficiente de atrito), a força de atrito é proporcional à força Normal do corpo. Existem dois tipos de atrito: o atrito estático e o cinético.
Atrito estático:
É a força de atrito que atua quando não ocorre deslizamentos dos corpos. A força de atrito estático máxima é a força minima para iniciar o movimento de um corpo. Quando o corpo não está em movimento a força de atrito deve ser maior que a força aplicada, então é usado o coeficiente de atrito estático.
Sua formula:
F = μe . N
Onde μe é o coeficiente de atrito estático e N é a força normal.
Atrito Cinético:
É a força de atrito que atua quando ocorre deslizamento dos corpos. Quando a força aplicada no corpo é maior que a força de atrito estático,ocorre movimento e consideramos sua força de atrito cinético ou dinâmico. A força de atrito cinético é sempre menor que a força aplicada, no calculo utilizamos o coeficiente de atrito estático.
Sua formula
F = μc . N
Onde μc é o coeficiente de atrito cinético e N a força normal.
Objetivos
O experimento tem como objetivo descobrir a força normal, e também descobrir a força de atrito estático máxima.
Materiais e Procedimentos
Foram utilizados nesse experimento um bloco, um transferidor, una tábua e uma régua.
Colocamos o bloco à 34,9cm de comprimento na régua. Com o transferidor colocado na base da tábua para fazer a variação dos graus, assim sabemos em quantos graus o bloco começa a deslizar.
Resultados
Px = P . sen35° => Px = m . g . sen35°
Py = P . cos35° => Py = n . g . cos35°
N = Py => N = m . g . cos35º
Fat = Px => Fat= m . g . sen35°
Fatmáx = μe . N
μe = Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{Fatmáx}{N}} => μe = Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{ m . g . sen35°}{m . g . cos35°}} => μe = Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{sen35°}{cos35°}} = 0,70.
N = m . g . cos35°
N = 0,08418 . 10 . cos35°
N = 0,69N
Fatmáx = μe . N
Fatmáx = 0,70 . 0,69
Fatmáx = 0,483N
Conclusão
Programação Scratch
Poligonos
Clique nos Links para ver os arquivos funcionando e explora-los mais a fundo.
1- Aprimorar o programa para desenhar polígonos regulares, permitindo que o usuário escolha quantos lados terá o polígono a ser desenhado.
2- Aprimore o programa incluindo um limite para o número de lados possíveis para o polígono, por exemplo, entre 3 e 12 lados. Use testes com Se/Então/Senão.
3- Aprimore o programa de forma a diminuir o número de passos do gatinho em função do número de lados do polígono, permitindo que o desenho caiba na área do palco, mesmo para polígonos com mais de 12 lados.
R: Concluindo as três questões obtemos o seguinte resultado:
4- Explique qual seria a lógica para que o gatinho desenhasse um círculo?
R: para que o gatinho desenhe um círculo, é necessário um numero muito grande de retas muito pequenas, divergindo o ângulo a cada reta, assim, no programa, o mais intuitivo de se fazer é, programar o gatinho para que ele de um passo, e vire 1° grau (sempre para o mesmo lado), repetindo 360 vezes, pois assim ele irá definir um circulo perfeito, concluindo os 360° graus do círculo. O arquivo a seguir contem vários polígonos e por final o gatinho define um círculo contendo todos os polígonos dentro
Movimento Retilíneo Uniforme
Referências
- ↑ HALLIDAY, David; RESNIK, Robert.Fundamentos da Física, 10 ed. LTC, 2016