Portfólio: João e Reinaldo
Portfólio: João e Reinaldo
- Curso
- Licenciatura em Física
- Disciplina
- Informática Aplicada ao Ensino de Física
- Professor
- Evandro Cantú
- Equipe
- João Carlos Munhoz das Neves
- Reinaldo Caceres
Atividade 1: O futuro da Internet
Há duas décadas a utilização da rede se popularizou graças à invenção da World Wide Web e da criação do grande primeiro navegador comercial: o Netscape.
A historiadora Elizabeth Eisenstein, autora do livro “The printing press as an agent of change” (a imprensa como um agente de mudança) faz uma analogia a meu ver muito acertada com a invenção de prensa de Gutemberg. Segundo ela, esta invenção mudou o mundo sob dois ponto relevantes:
- a) A capacidade de duplicação das informações própria da imprensa.
- b) A preservação do conhecimento.
Essa “condição de permanência" da informação impressa provocou uma mudança progressiva no mundo, ou seja, "a preservação do velho foi um requisito para que se criasse a tradição do novo.” Atualmente é impossível imaginar por quantas mil vezes a internet multiplicou estes efeitos do livro impresso na evolução do mundo desde o Netscape.
Hoje, sem dúvida a nossa vida não é mais como antes. Tudo é mais fácil, o mundo ao alcance dos dedos. E a comodidade do cidadão comum juntou-se aos interesses financeiros, fazendo com que, hoje por exemplo, durante uma greve de ba
1.1.1 Associação em série de resistores 1.1.2 Associação em paralelo de resistores
1.2 Divisor de Tensão
1.2.1 Aplicação do Divisor de Tensão
1.3 Código de cores de resistores 1.4 Aplicativos interessantes para smartphones e tabletsncários os bancos funcionem (quase) normalmente. Um vigilante amigo meu comentava que na agencia onde ele trabalha, a situação está tensa. Tem que manter os grevistas sob vigilância cerrada, pois cada um deles que se afasta pode ser a sua oportunidade de mandar trazer um cafezinho da lanchonete ao lado.
Se toda esta mudança ocorreu em apenas 20 anos, como prever a internet no mundo daqui a 100 anos? Talvez a internet como nós a conhecemos não exista mais. Uma coisa já está clara: nossos computadores com teclado, mouse e monitor serão alvo de riso dos adolescentes em visita a museus já num futuro próximo. Como já hoje acontece com a minha contemporânea, ultra moderna e imensa máquina de escrever elétrica da IBM.
É claro que sempre há uma pergunta funesta e apolíptica no ar: e se der uma pane na internet? Uma prévia sem maiores consequências ocorreu na virada do século XX, quando multidões de funcionários permaneceram em seus postos nas grande companhias, festejando o reveillon com peru regado a champagne do patrão, sob o pretexto de esperar o bug do milênio. Mais um mérito da internet, que nesta noite proporcionou pretexto a muitos maridos procurarem o tal bug só deus sabe onde.
Nesta semana aconteceu em Foz do Iguaçu o XXIII SNPTEE (Seminário Nacional de Produção e Transmissão de Energia Elétrica), reunindo todas as entidades que detém a tecnologia de ponta do setor no mundo. Do mundo todo. E a internet com isto?
Acontece que num evento como este fica claro que hoje, tão importante quanto imensos geradores das usinas, estão os sistemas de controle de geração, transmissão e distribuição de energia elétrica. Não existe mais um sistema destes que funcione de forma isolada, todo o gigantesco volume de energia elétrica que circula no planeta é totalmente gerenciado por sistemas automatizados, que só funcionam conectados em rede.
Enfim, um leigo como eu consideraria a energia elétrica é muito mais vital para o mundo do que a internet. Mas se hoje já é impossível imaginar a existência da energia elétrica sem os recursos da internet, será possível existir o mundo daqui a 100 anos sem a internet?
- Comentários
- Ficou bom o texto. --Evandro.cantu (discussão) 10h23min de 29 de outubro de 2015 (BRST)
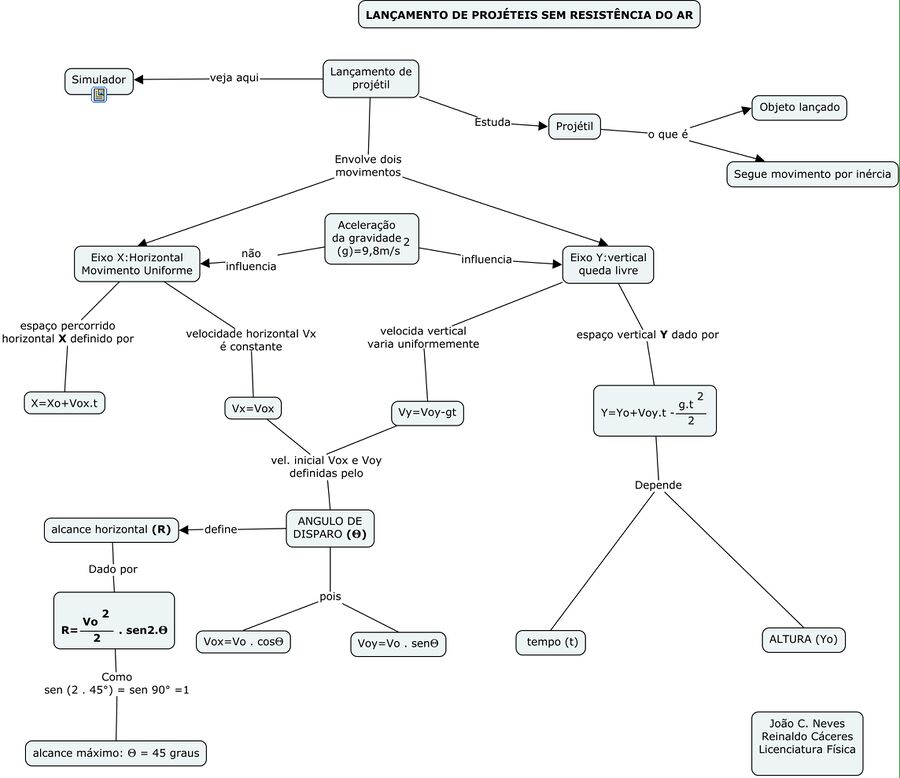
Atividade 2: Mapa conceitual: Lançamento de projéteis
Movimento de um projétil:O movimento de um projétil sob a ação da gravidade em duas dimensões pode ser considerado como resultante da composição (soma vetorial) de dois movimentos unidimensionais independentes: um movimento retilíneo uniforme (MRU), ao longo da direção x, e um movimento retilíneo uniformemente variado (MRUV), ao longo da direção y. O MRU é a projeção do deslocamento do corpo no eixo horizontal, ou seja, o movimento da sombra do projétil se ele fosse iluminado de cima para baixo. O MRUV é a projeção do deslocamento do corpo na direção vertical, ou seja, o movimento da sombra do projétil sobre o eixo y, se o projétil fosse iluminado da direita para a esquerda. A função horária genéricas do MRU ao longo da direção x é:
X = X 0 +V x .t
Sendo x a posição do corpo no instante t, x0 a posição no instante inicial t0, Vx = v0x a velocidade média, v0 a velocidade no instante t0, e t o instante no qual se queira saber a posição do corpo. As funções horárias genéricas do MRUV ao longo da direção y são:
y = yo + vot 1 ay t² , Vy = Voy + ay t
No mapa conceitual abaixo estão relacionadas as grandezas envolvidas no estudo destes dois movimentos.
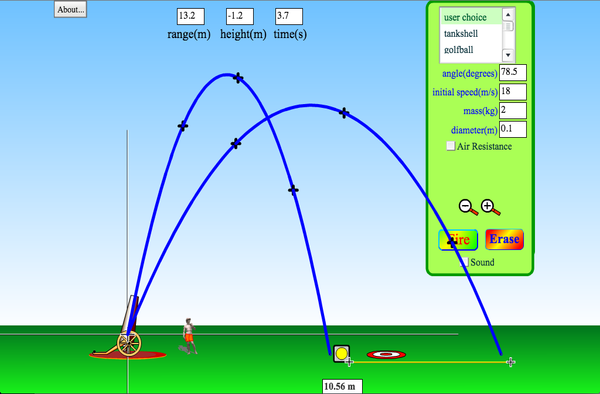
simulador lançamento de projéteis
Atividade 3: Pagina WIKI integrada com Mapas Conceituais
Inserir fórmulas
- Espaço em função do tempo no MRUV (Movimento Uniforme)
- Coeficiente de Pearson
- Indica nível de correlação entre duas variáveis.
Falhou ao verificar gramática (função desconhecida '\sqrtyi'): {\displaystyle r = {\frac{\sum(xi-x)*(yi-y)}{{\sqrt{sum[(xi-x)]^2}{[\sqrtyi-y)]^2}}
- Aceleração no MRUV
Tabela
| Nº | y(m) | t² |
| 1 | 0,20 | 0,02 |
| 2 | 0,40 | 0,05 |
| 3 | 0,60 | 0,07 |
| 4 | 0,80 | 0,10 |
Atividade 3: Pagina WIKI integrada com Mapas Conceituais
Inserir fórmulas
- Espaço em função do tempo no MRUV (Movimento Uniforme)
- Coeficiente de Pearson
- Indica nível de correlação entre duas variáveis.
Falhou ao verificar gramática (função desconhecida '\sqrtyi'): {\displaystyle r = {\frac{\sum(xi-x)*(yi-y)}{{\sqrt{sum[(xi-x)]^2}{[\sqrtyi-y)]^2}}
- Aceleração no MRUV
Tabela
| Nº | y(m) | t² |
| 1 | 0,20 | 0,02 |
| 2 | 0,40 | 0,05 |
| 3 | 0,60 | 0,07 |
| 4 | 0,80 | 0,10 |
Atividade 4: Simulador Scratch
Simulador MRU
Construa uma simulação para o MRUV. Mídia:joao_MRUV 01.sb
Projeto de Aplicação com programação Scratch
Construa uma aplicação no Scratch para traçar o gráfico do movimento oblíquo no vácuo, ilustrando um lançamento de projétil, com possibilidade de escolha da velocidade inicial (v0) e do ângulo de lançamento (Θ).
Mídia:joao_PROJETIL_Final c sensor.sb
Atividade 5: gráficos com planilhas de cálculo
Exemplo de Planilha e gráfico MRUV
Exercicios: 1) Um móvel se desloca em MRUV com aceleração constante de 1,2 m/s. No instante t = 0 s, a velocidade do móvel era 4 m/s e ocupara a posição s = 8m. Construa na Planilha de Cálculo os gráficos de v(t) e s(t) para o tempo entre 0 e 10 s.