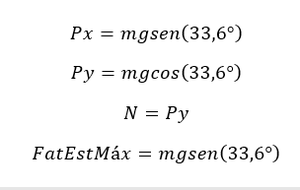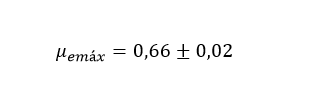Portfólio: PatiNando: mudanças entre as edições
| (47 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 7: | Linha 7: | ||
* Patrícia Reis | * Patrícia Reis | ||
=Experimento: Tempo de Reação Humana= | ==Experimento: Tempo de Reação Humana== | ||
O tempo de reação humana, também chamada de reflexo, caracteriza-se pelo intervalo de tempo gasto no envio de uma mensagem do sistema nervoso ao cérebro e na reação física do corpo ao estimulo. O objetivo desse experimento é determinar o tempo de reação humana com resultados a partir de um movimento de queda livre. | O tempo de reação humana, também chamada de reflexo, caracteriza-se pelo intervalo de tempo gasto no envio de uma mensagem do sistema nervoso ao cérebro e na reação física do corpo ao estimulo. O objetivo desse experimento é determinar o tempo de reação humana com resultados a partir de um movimento de queda livre. <ref>HALLIDAY, David; RESNIK, Robert; WALKER, Jearl. '''Fundamentos da Física''', 10 ed. LTC, 2016. </ref> <ref>MAXIMO, A.; ALVARENGA, B., '''Física: volume único'''. Scipione, 1997 </ref> | ||
;[[Mídia:relatoriopatinando1.pdf|Tempo de Reação Humana]] | ;[[Mídia:relatoriopatinando1.pdf|Tempo de Reação Humana]] | ||
=Experimento: Gráficos com Planilha de Cálculo= | [http://200.17.101.9:8080/rid=1SY70336Z-631R87-WT/MapaPatiNando.cmap] | ||
==Experimento: Gráficos com Planilha de Cálculo== | |||
Neste experimento considerou-se um conjunto de dados e realizou-se gráficos para cada situação. | Neste experimento considerou-se um conjunto de dados e realizou-se gráficos para cada situação. | ||
| Linha 19: | Linha 21: | ||
;[[Mídia:Calcpatinando.ods|Gráficos]] | ;[[Mídia:Calcpatinando.ods|Gráficos]] | ||
=Experimento: Plano Inclinado= | ==Experimento: Plano Inclinado== | ||
===Introdução=== | ===Introdução=== | ||
| Linha 35: | Linha 37: | ||
'''Material''': Calha com inclinação variável, esfera cronômetro, régua ou trena. | '''Material''': Calha com inclinação variável, esfera cronômetro, régua ou trena. | ||
Procedimentos: Inicialmente graduou-se a calha em intervalos de 10 cm, com o auxílio de um cronômetro e um celular gravou-se o movimento descrito pela bolinha ao longo da calha e também o cronometro. Para a construção do gráfico e extração do tempo, foi considerado o instante em que a bolinha encostou em cada uma das linhas (da graduação na calha), em seguida realizou-se uma adequação em cada instante extraído para encontrar a diferença temporal e assim obter os valores em cada momento. Com os valores encontrados calcula-se a média dos tempos e constrói-se o gráfico. Para determinar uma possível equação do movimento a partir dos valores médios encontrados e do gráfico é feita uma aproximação por uma função quadrática considerando a relação . Conhecendo o tempo e a posição pode se encontrar a aceleração e com isso escrever uma equação que aproxima do movimento. | Procedimentos: Inicialmente graduou-se a calha em intervalos de 10 cm, com o auxílio de um cronômetro e um celular gravou-se o movimento descrito pela bolinha ao longo da calha e também o cronometro. Para a construção do gráfico e extração do tempo, foi considerado o instante em que a bolinha encostou em cada uma das linhas (da graduação na calha), em seguida realizou-se uma adequação em cada instante extraído para encontrar a diferença temporal e assim obter os valores em cada momento. Com os valores encontrados calcula-se a média dos tempos e constrói-se o gráfico. Para determinar uma possível equação do movimento a partir dos valores médios encontrados e do gráfico é feita uma aproximação por uma função quadrática considerando a relação s = s<sub>0</sub> + v<sub>0</sub> t + 1/2 a t<sup>2</sup> . Conhecendo o tempo e a posição pode se encontrar a aceleração e com isso escrever uma equação que aproxima do movimento. | ||
Tomando os valores médios apresentados na tabela determinou-se o valor da aceleração a partir da relação acima e obteve-se: | Tomando os valores médios apresentados na tabela determinou-se o valor da aceleração a partir da relação acima e obteve-se: a=0,1199 m/s<sup>2</sup> | ||
Logo, a equação que pode descrever o gráfico é: | Logo, a equação que pode descrever o gráfico é: | ||
s=0, | s=0,12t<sup>2</sup> para valores de dados em segundo e em metros. | ||
===Resultados e Planilha=== | |||
Com base na planilha abaixo | |||
[[Mídia:PlanilhaPatinando.ods|Planilha com Dados e Gráfico]] | |||
[[Arquivo:figuramediçãopatinando.png]] | |||
Obteve-se os seguintes valores: | |||
Velocidade média nos primeiros 20 cm: 0,1244 m/s | |||
Velocidade média nos últimos 20 cm: 0,4319 m/s. | |||
===Conclusões=== | ===Conclusões=== | ||
Com o o presente relatório é possível visualizar um ponto muito próximo da iminência de movimento e estimar o valor do coeficiente de atrito, assim a teoria vista na aula se completa com a prática laboratorial desencadeando uma melhor compreensão. O presente documento também ressalta a importância da medição correta e da verificação dos cálculos e dados para que o valor alcançado se aproxime do ideal teórico. | |||
==Experimento: Determinação do Coeficiente de Atrito Estático no Plano inclinado== | |||
Os Participantes deste experimento foram: | |||
Cristopher | |||
Evandro Andretti | |||
Fernando Reis | |||
Patricia Reis | |||
Pedro Reis | |||
===Introdução=== | |||
'''Força de Atrito''' | |||
A força de atrito é uma força que se opõe ao movimento dos corpos. Ela pode ser estática, se o corpo estiver em repouso, ou dinâmica, para corpos em movimento. <ref>HALLIDAY, David; RESNIK, Robert; WALKER, Jearl. '''Fundamentos da Física''', 10 ed. LTC, 2016. </ref> <ref>MAXIMO, A.; ALVARENGA, B., '''Física: volume único'''. Scipione, 1997 </ref> | |||
Considere um corpo que é puxado, porém não consegue escorregar na superfície, significa que ele recebeu a ação de uma força de atrito que impede seu movimento. Essa força é denominada atrito estático. Nesse caso: | |||
F = FAE | |||
A força de atrito estático tem um limite máximo, denominado tem um limite máximo, denominado de força de atrito estático máximo. | |||
FAEmax = μe . N | |||
N é a força normal que o corpo troca com a superfície do apoio; | |||
μe é o coeficiente de atrito estático. | |||
O coeficiente é um numero adimensional que depende das rugosidades da face do corpo que está apoiada e da superfície de contato. Quanto mais áspero for o corpo ou a superfície maior será o coeficiente. | |||
A força de atrito estático pode variar de zero ate seu limite máximo, em função da intensidade da força aplicada. Então o corpo so deslizará na superfície quando a força F vencer o atrito estático. | |||
'''Atrito Dinâmico''' | |||
Também chamado de atrito cinético, o atrito dinâmico ocorre quando a força do atrito estático for superada, de modo que os dois corpos entram em movimento, gerando, assim, uma menor força de atrito, por exemplo, empurrar a pedra depois que ela entrou em movimento. | |||
Para calcular a força do atrito dinâmico, utiliza-se a expressão: Fatd = μd.N, donde μd corresponde ao coeficiente do atrito dinâmico e N, a força normal. | |||
===Objetivo=== | |||
Determinar um valor experimental para o coeficiente de atrito estático máximo sem o auxílio de um dinamômetro (desconhecendo o peso do objeto) utilizando como instrumentos de medida apenas régua e transferidor. | |||
===Materiais e Métodos=== | |||
Os materiais utilizados neste experimento: | |||
1. Plano inclinado | |||
2. Régua | |||
3. Transferidor | |||
4. Corpo de prova | |||
5. Calculadora | |||
6. Caneta e papel | |||
Para realizar a atividade inicialmente foi determinado qual a posição próxima da iminência de movimento do corpo no plano inclinado. Com esta posição determinada foi calculado inicialmente de duas formas diferentes para obter o ângulo de abertura, a primeira maneira foi com o auxílio da régua e determinou-se os valores do triângulo formado (ver imagens abaixo) e com isso o ângulo formado. A segunda forma foi medindo diretamente o ângulo com o auxílio do transferidor considerando o triângulo interno (ver figuras abaixo) que é semelhante ao triângulo externo. Com o método que melhor representa o ângulo encontrado repetiu-se o experimento um total de 10 vezes. | |||
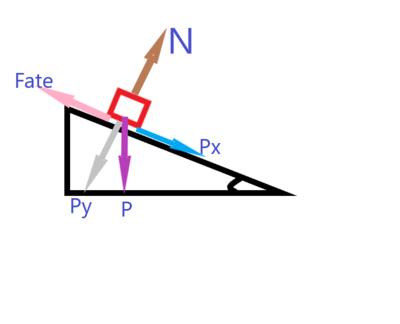
Considerando então o problema, desenhou-se um esboço para indicar as forças de atuação para em seguida construir o diagrama de corpo livre: | |||
o ângulo entre Py e P é o mesmo ângulo do triângulo que determinou-se nas medidas e que consideraremos para apresentação o valor da média 33,6°. | |||
[[Arquivo:diagrama1patinandoatritoestatico.png|400px]] | |||
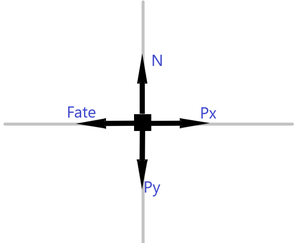
Com o desenho em mãos obteve-se o diagrama de corpo livre abaixo: | |||
[[Arquivo:diagramacorpolivrepatinandoatritoestatico.png|300px]] | |||
De posse do diagrama de corpo livre e do valor do ângulo, determinar o coeficiente de atrito estático tornou-se consequência natural, decompôs-se o peso P em Px e Py onde o primeiro foi dado por Px=P.sen(33,6°) e Py=P.cos(33,6°). Considerando o sistema em equilíbrio equacionou-se as forças no eixo x e no eixo y onde obteve-se que o coeficiente de atrito estático coincide com a tangente do ângulo calculado. | |||
[[Arquivo:dadoscoefpatinandoestatico.png|300px]] | |||
====Imagens==== | |||
[[Arquivo:imagemexperimentocoeficientedeatritoestaticopatinando(1).jpeg|400px]] | |||
[[Arquivo:imagemexperimentocoeficientedeatritoestaticopatinando(2).jpeg|400px]] | |||
[[Arquivo:imagemexperimentocoeficientedeatritoestaticopatinando(4).jpeg|400px]] | |||
===Reultados=== | |||
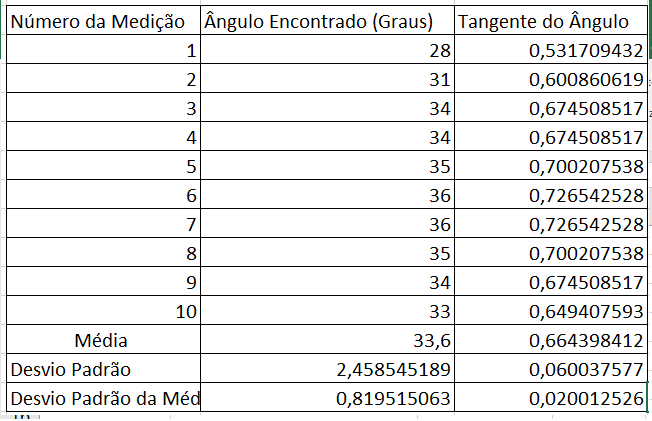
Como viu-se que o coeficiente de atrito estático máximo acaba sendo definido pela tangente do ângulo abaixo apresenta-se uma tabela com o valor das medições e o tratamento estatístico de desvio padrão e desvio padrão da média tanto para o ângulo quanto para a tangente. | |||
[[Arquivo:planilhacoeficientepatinando.png]] | |||
assim, neste experimento obteve-se o valor de | |||
[[Arquivo:coefatriestmaxpatinandohenry.png]] | |||
===Conclusão=== | |||
Assim foi determinado o coeficiente de atrito estático máximo para este caso experimentalmente e obteve-se um erro pouco maior que 3% que é aceitável. | |||
O erro sempre existirá o que pode-se fazer é melhorar a qualidade da medição e o tratamento dado aos dados a fim de diminuir ao máximo esta questão. O experimento mostrou-se eficaz na determinação este coeficiente de atrito e é uma atividade indicada também para o ensino médio para que os alunos entendam esta força presente e necessária. | |||
==Referências== | ==Referências== | ||
<references /> | <references /> | ||
---- | ---- | ||
[[Categoria:Portfólio Licenciatura]] | [[Categoria:Portfólio Licenciatura]] | ||
Edição atual tal como às 23h18min de 9 de outubro de 2018
Portfólio: PatiNando
- Curso
- Licenciatura em Física
- Disciplina
- Informática Aplicada ao Ensino de Física
- Professor
- Evandro Cantú
- Equipe
- Fernando Reis
- Patrícia Reis
Experimento: Tempo de Reação Humana
O tempo de reação humana, também chamada de reflexo, caracteriza-se pelo intervalo de tempo gasto no envio de uma mensagem do sistema nervoso ao cérebro e na reação física do corpo ao estimulo. O objetivo desse experimento é determinar o tempo de reação humana com resultados a partir de um movimento de queda livre. [1] [2]
Experimento: Gráficos com Planilha de Cálculo
Neste experimento considerou-se um conjunto de dados e realizou-se gráficos para cada situação.
Experimento: Plano Inclinado
Introdução
O plano inclinado é um exemplo de máquina simples. Trata-se de uma superfície plana cujos pontos de início e fim estão a alturas diferentes.
Objetivos
Neste experimento iremos realizar medidas simples para cálculo da velocidade média e instantânea. Utilizaremos como aparato experimental uma bolinha que desce por uma calha inclinada. Temos como objetivo analisar o movimento de uma bolinha ao descer a calha, calcular sua velocidade média e elaborar um procedimento experimental para estimar a velocidade instantânea.
Materiais e Procedimentos
Material: Calha com inclinação variável, esfera cronômetro, régua ou trena.
Procedimentos: Inicialmente graduou-se a calha em intervalos de 10 cm, com o auxílio de um cronômetro e um celular gravou-se o movimento descrito pela bolinha ao longo da calha e também o cronometro. Para a construção do gráfico e extração do tempo, foi considerado o instante em que a bolinha encostou em cada uma das linhas (da graduação na calha), em seguida realizou-se uma adequação em cada instante extraído para encontrar a diferença temporal e assim obter os valores em cada momento. Com os valores encontrados calcula-se a média dos tempos e constrói-se o gráfico. Para determinar uma possível equação do movimento a partir dos valores médios encontrados e do gráfico é feita uma aproximação por uma função quadrática considerando a relação s = s0 + v0 t + 1/2 a t2 . Conhecendo o tempo e a posição pode se encontrar a aceleração e com isso escrever uma equação que aproxima do movimento. Tomando os valores médios apresentados na tabela determinou-se o valor da aceleração a partir da relação acima e obteve-se: a=0,1199 m/s2
Logo, a equação que pode descrever o gráfico é: s=0,12t2 para valores de dados em segundo e em metros.
Resultados e Planilha
Com base na planilha abaixo Planilha com Dados e Gráfico
Obteve-se os seguintes valores:
Velocidade média nos primeiros 20 cm: 0,1244 m/s Velocidade média nos últimos 20 cm: 0,4319 m/s.
Conclusões
Com o o presente relatório é possível visualizar um ponto muito próximo da iminência de movimento e estimar o valor do coeficiente de atrito, assim a teoria vista na aula se completa com a prática laboratorial desencadeando uma melhor compreensão. O presente documento também ressalta a importância da medição correta e da verificação dos cálculos e dados para que o valor alcançado se aproxime do ideal teórico.
Experimento: Determinação do Coeficiente de Atrito Estático no Plano inclinado
Os Participantes deste experimento foram:
Cristopher
Evandro Andretti
Fernando Reis
Patricia Reis
Pedro Reis
Introdução
Força de Atrito
A força de atrito é uma força que se opõe ao movimento dos corpos. Ela pode ser estática, se o corpo estiver em repouso, ou dinâmica, para corpos em movimento. [3] [4]
Considere um corpo que é puxado, porém não consegue escorregar na superfície, significa que ele recebeu a ação de uma força de atrito que impede seu movimento. Essa força é denominada atrito estático. Nesse caso:
F = FAE
A força de atrito estático tem um limite máximo, denominado tem um limite máximo, denominado de força de atrito estático máximo.
FAEmax = μe . N
N é a força normal que o corpo troca com a superfície do apoio; μe é o coeficiente de atrito estático.
O coeficiente é um numero adimensional que depende das rugosidades da face do corpo que está apoiada e da superfície de contato. Quanto mais áspero for o corpo ou a superfície maior será o coeficiente. A força de atrito estático pode variar de zero ate seu limite máximo, em função da intensidade da força aplicada. Então o corpo so deslizará na superfície quando a força F vencer o atrito estático.
Atrito Dinâmico
Também chamado de atrito cinético, o atrito dinâmico ocorre quando a força do atrito estático for superada, de modo que os dois corpos entram em movimento, gerando, assim, uma menor força de atrito, por exemplo, empurrar a pedra depois que ela entrou em movimento.
Para calcular a força do atrito dinâmico, utiliza-se a expressão: Fatd = μd.N, donde μd corresponde ao coeficiente do atrito dinâmico e N, a força normal.
Objetivo
Determinar um valor experimental para o coeficiente de atrito estático máximo sem o auxílio de um dinamômetro (desconhecendo o peso do objeto) utilizando como instrumentos de medida apenas régua e transferidor.
Materiais e Métodos
Os materiais utilizados neste experimento: 1. Plano inclinado 2. Régua 3. Transferidor 4. Corpo de prova 5. Calculadora 6. Caneta e papel
Para realizar a atividade inicialmente foi determinado qual a posição próxima da iminência de movimento do corpo no plano inclinado. Com esta posição determinada foi calculado inicialmente de duas formas diferentes para obter o ângulo de abertura, a primeira maneira foi com o auxílio da régua e determinou-se os valores do triângulo formado (ver imagens abaixo) e com isso o ângulo formado. A segunda forma foi medindo diretamente o ângulo com o auxílio do transferidor considerando o triângulo interno (ver figuras abaixo) que é semelhante ao triângulo externo. Com o método que melhor representa o ângulo encontrado repetiu-se o experimento um total de 10 vezes.
Considerando então o problema, desenhou-se um esboço para indicar as forças de atuação para em seguida construir o diagrama de corpo livre: o ângulo entre Py e P é o mesmo ângulo do triângulo que determinou-se nas medidas e que consideraremos para apresentação o valor da média 33,6°.
Com o desenho em mãos obteve-se o diagrama de corpo livre abaixo:
De posse do diagrama de corpo livre e do valor do ângulo, determinar o coeficiente de atrito estático tornou-se consequência natural, decompôs-se o peso P em Px e Py onde o primeiro foi dado por Px=P.sen(33,6°) e Py=P.cos(33,6°). Considerando o sistema em equilíbrio equacionou-se as forças no eixo x e no eixo y onde obteve-se que o coeficiente de atrito estático coincide com a tangente do ângulo calculado.
Imagens
Reultados
Como viu-se que o coeficiente de atrito estático máximo acaba sendo definido pela tangente do ângulo abaixo apresenta-se uma tabela com o valor das medições e o tratamento estatístico de desvio padrão e desvio padrão da média tanto para o ângulo quanto para a tangente.
assim, neste experimento obteve-se o valor de
Conclusão
Assim foi determinado o coeficiente de atrito estático máximo para este caso experimentalmente e obteve-se um erro pouco maior que 3% que é aceitável. O erro sempre existirá o que pode-se fazer é melhorar a qualidade da medição e o tratamento dado aos dados a fim de diminuir ao máximo esta questão. O experimento mostrou-se eficaz na determinação este coeficiente de atrito e é uma atividade indicada também para o ensino médio para que os alunos entendam esta força presente e necessária.
Referências
- ↑ HALLIDAY, David; RESNIK, Robert; WALKER, Jearl. Fundamentos da Física, 10 ed. LTC, 2016.
- ↑ MAXIMO, A.; ALVARENGA, B., Física: volume único. Scipione, 1997
- ↑ HALLIDAY, David; RESNIK, Robert; WALKER, Jearl. Fundamentos da Física, 10 ed. LTC, 2016.
- ↑ MAXIMO, A.; ALVARENGA, B., Física: volume único. Scipione, 1997