App Inventor: Simulando um plano inclinado
App Inventor: Aplicativos para resolver equações do 1o e 2o graus
Vamos utilizar o App Inventor vamos desenvolver um aplicativo para determinar as raízes de uma Equação do 1o Grau:
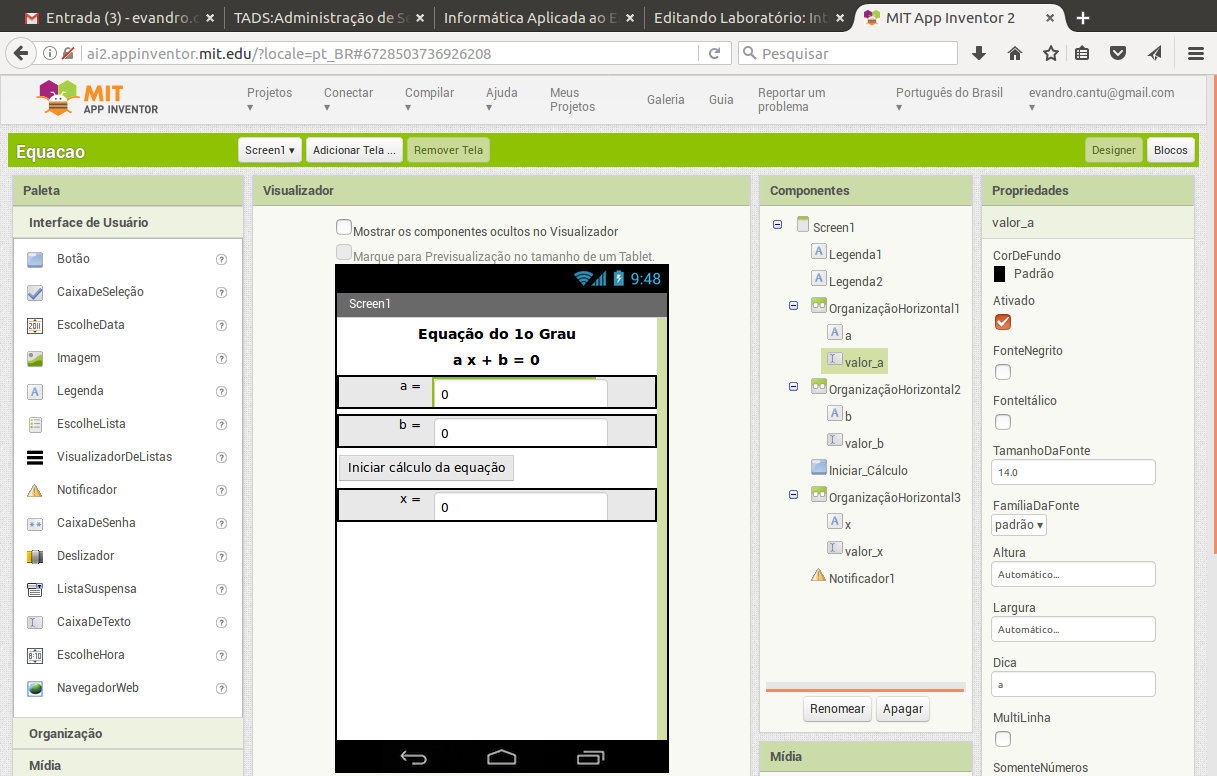
- Tela Designer
- Na tela Designer foram incluídos Legendas para identificar a aplicação e o nome das váriáveis, CaixasDeTexto para entrada dos parâmetros da equação e um Botão para iniciar o cálculo da equação.
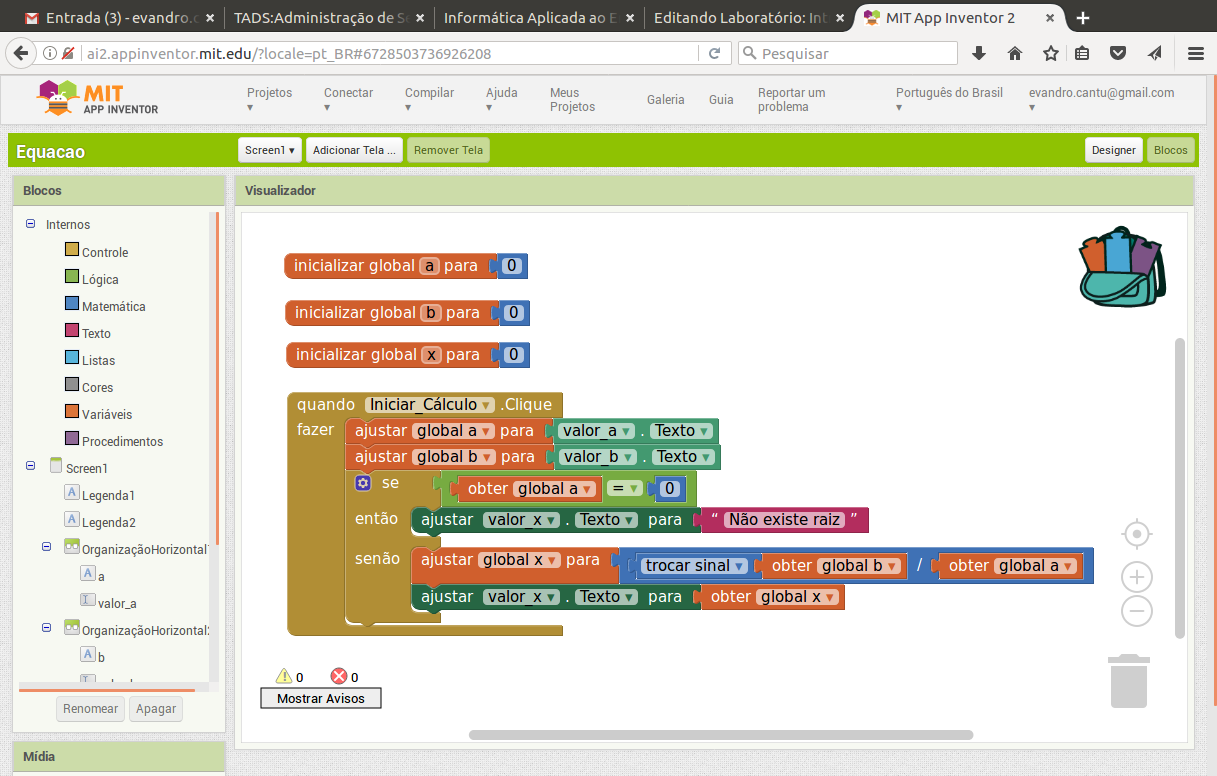
- Tela Blocos
Na tela Blocos está a lógica para extrair as raízes da equação do 1o grau. Foram criadas váriáveis globais para os parâmetros e variáveis da equação, e uma função que será executada quando o botão for clicado.
Exercícios
- Construa um aplicativo para determinar as raízes de uma Equação do 2o Grau.
- Construa um aplicativo para calcular a taxa de gordura de uma pessoa a partir dos dados de peso e altura.
Plano Inclinado
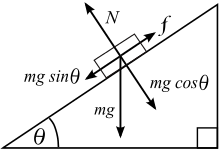
Quando colocamos um corpo sobre um plano inclinado, sem atrito, o corpo deslizará para baixo no plano pela ação da gravidade.
No plano inclinado a força gravitacional atua com duas componentes:
- Força perpendicular ao plano (m g cosΘ): esta componente tem intensidade igual, porém sentido oposto à força normal N exercida pelo plano sobre o objeto. Não há movimento perpendicular ao plano;
- Força paralela ao plano (m g senΘ), responsável por fazer o objeto deslizar para baixo no plano inclinado.
- Aceleração do corpo no plano inclinado
- O corpo vai deslizar para baixo no plano inclinado com aceleração:
a = g senΘ
O movimento do corpo, portando, segue as características do MRUV:
s = s0 + v0 t + a t2 / 2
- ou, considerando s0 = 0, v0 = 0 e a = g senΘ:
s = g senΘ t2 / 2
Simulação de um Plano Inclinado na tela do dispositivo móvel
Vamos construir uma aplicação para o dispositivo móvel que simule um plano inclinado. Para tal, vamos utilizar o sensor de 0rientação do dispositivo móvel, o qual oferece informações sobre a orientação tridimensional da tela do dispositivo.
Sensor de Orientação do AppInventor
O Sensor de Orientação oferece informações sobre a orientação tridimensional do dispositivo móvel através de três parâmetros:
- Rolagem
- Ângulo de inclinação lateral do dispositivo:
- 0 grau com o dispositivo nivelado;
- Aumenta para 90 graus a medida que o lado direito é levantado;
- Diminui para -90 graus a medida que o lado esquerdo é levantado.
- Altura
- Ângulo de inclinação longitudinal do dispositivo:
- 0 grau com o dispositivo nivelado;
- Aumenta para 90 graus a medida que o topo do dispositivo é levantado;
- Diminui para -90 graus a medida que a base do dispositivo é levantada.
- Azimute
- Ângulo orientação em relação ao norte magnético da terra:
- 0 grau quando o dispositivo aponta para o norte;
- 90 graus quando o dispositivo aponta para o leste;
- 180 graus quando o dispositivo aponta para o sul;
- 270 graus quando o dispositivo aponta para o oeste.
Exercício
Construa com o AppInventor um aplicativo utilizando o Sensor de Orientação e a guia Desenho e Animação, utilizando uma Pintura de fundo de tela e uma Bola que funcione da seguinte forma:
- Quando a tela for tocada, mover a Bola para a coordenada da tela que foi tocada;
- Quando o celular for movimentado, utilizar os ângulos relativos a Rolagem e Altura para que a Bola se movimente na tela de acordo com as relações matemáticas da física relativas a um Plano Inclinado.
Referências
Root (discussão) 20h16min de 6 de novembro de 2023 (UTC)