Árvores

Árvores

Uma árvore binária é uma estrutura de dados formada por um conjunto finito de elementos ou nós. Uma árvore pode estar vazia ou pode ser formada por um nó chamado raiz e dois sub-conjuntos de elementos chamados sub-árvore esquerda e sub-árvore direita. As sub-árvores esquerda e direita são também árvores binárias e podem estar vazias .

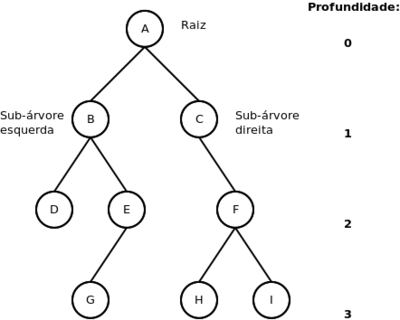
A figura abaixo ilustra uma árvore binária :

Na figura:

• O nó raiz A tem duas sub-árvores B e C;
• O nó B tem duas sub-árvores D e E;
• O nó C tem apenas a sub-árvore da direita F;
• O nó E tem apenas a sub-árvore da esquerda G;
• O nó F tem duas sub-árvores H e I;
• Os nós D, G, H e I não tem sub-árvores, portanto, são chamados folhas.

Se A tem duas sub-árvores B e C, diz-se que:

• A é pai de B e C;
• B é filho esquerdo de A;
• C é filho direito de A.
• B é irmão de C.

Profundidade da árvore binária

Numa árvore binária, o nó raiz é considerado como profundidade 0 (zero). As sub-árvores do nó raiz profundidade 1, e assim sucessivamente. No exemplo da figura, a árvore binária tem profundidade 3.

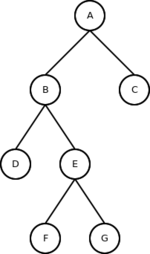
Árvore estritamente binária

Uma árvore é estritamente binária se todo nó que não for folha tenha as sub-árvores direita e esquerda não vazias.

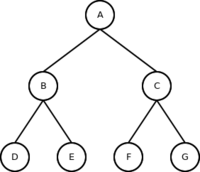
Árvore binária completa

Uma árvore é binária completa se for uma árvore estritamente binária e todas as folhas estiverem na mesma profundidade.

Aplicações das árvores binárias

As árvores binárias são uma estrutura de dados útil quando precisam ser tomadas decisões bi-direcionais em cada ponto do processo. Por exemplo, suponha que queiramos encontrar repetições em uma lista de números. Uma maneira de fazer isto é comparar cada número com todos os que o precedem. Entretanto, isto pode envolver muitas comparações. Outra maneira é utilizar uma árvore binária .

Exemplo

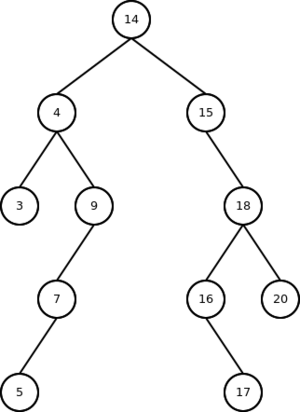
Suponha que temos a seguinte lista de números para verificar repetições:

14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Neste caso, iniciamos a árvore com o primeiro número da lista como sendo o nó raiz. Na sequência, comparamos o próximo número com o número da raiz, se for igual é uma repetição. Se for menor, comparamos com a sub-árvore da esquerda. Se for maior, comparamos com a sub-árvore da direita. Se a sub-árvore estiver vazia, incluímos o número como filho desta sub-árvore, caso seja menor ou maior, da mesma forma que foi realizado no início.

Veja a árvore que seria construída neste exemplo:

Percorrendo uma árvore

Uma operação importante em uma árvore binária é percorrer todos os seus nós.

Diferentemente de uma lista, na qual os nós são percorridos de maneira linear, numa árvore, existem diferentes ordens para poder percorrê-la.

Todos os métodos para percorrer uma árvore são definidos recursivamente, de modo que percorrer uma árvore envolve visitar a raiz e depois a sub-árvore direita e a esquerda. O que difere cada método é a ordem em que estas operações são realizadas .

Ordem esquerda-raiz-direita

Nesta ordem, percorre-se primeiro a sub-árvore esquerda, na ordem esquerda-raiz-direita. Depois a raiz. E depois a sub-árvore direita, também na ordem esquerda-raiz-direita.

Por exemplo, dada a árvore:

      A
     / \
    B   C
   /   / \
  D   E   F
 / \   \
G   H   I

a de ordem de varredura esquerda-raiz-direita é :

      5
     / \
    3   8
   /   / \
  1   6   9
 / \   \
0   2   7

Implementação de árvores em linguagem C

Cada nó de uma árvore pode ser implementado em linguagem C como uma estrutura com três campos: um campo conteúdo, para guardar a informação deste nó, e dois campos tipo ponteiro que apontam para as sub-árvores direita e esquerda.

Declaração de um nó de uma árvore

typedef struct arvore {
       int    conteudo;
       struct arvore *esq;
       struct arvore *dir;
} arvore;

Referência: .

Note que a declaração do nó da árvore é recursiva, onde os ponteiros *esq e *dir apontam para estruturas do mesmo tipo que está sendo declarada.

Endereço de uma árvore e definição recursiva

O endereço de uma árvore binária é o endereço de sua raiz .

main()
{
  arvore *r; //r é um ponteiro para uma árvore
  ...
}

Uma árvore binária pode ser definida de maneira recursiva, como segue:

Um objeto r é uma árvore binária se:

1. r é NUL ou
2. r->esq e r->dir são árvores binárias.

Percorrer árvore binária na ordem esquerda-raiz-direita

Função recursiva que faz a varredura e-r-d de uma árvore binária:

void erd(arvore *r) {
    if (r != NULL) {
       erd(r->esq);
       printf("%d\n", r->conteudo);
       erd(r->dir); 
    }
}

Inserção em árvores binárias

Função para inserção em árvore binária:

void inserir(arvore *r, int num){
     if(r == NULL){
        r = (arvore *) malloc(sizeof(arvore));
        r->esq = NULL;
        r->dir = NULL;
        r->conteudo = num;
     }else{
         if(num < r->conteudo)  
              inserir(r->esq, num));
         else  
              inserir(r->dir, num));
     }
 }

Referência:

Referências

---

--Evandro.cantu (discussão) 09h43min de 11 de novembro de 2014 (BRST)

---