Sistemas de Controle

Sistemas de Controle

Referência principal

OGATA, Katsuhiko. Engenharia de Controle Moderno, 5^a Ed, Pearson, 2011. .

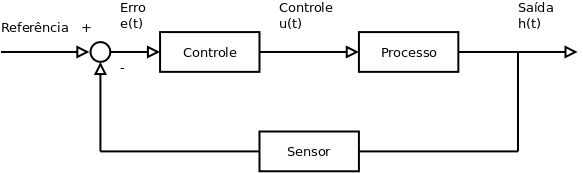
Um sistema de controle em malha fechada procura manter a saída do sistema alinhada com uma referência. Para tal, monitora uma variável do sistema com um sensor e compara com a referência. O erro resultante é utilizado para ajustar a ação de controle (, p. 7).

Controle On / Off

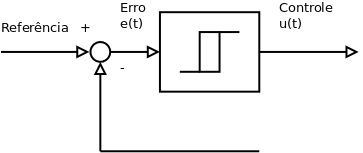
O controle on/off procura ajustar a saída do sistema com a referência ligando e desligando a ação de controle. Por exemplo, para manter uma dada temperatura em um forno, liga ou desliga a resistência de aquecimento, caso a temperatura fique abaixo ou acima do ponto de referência, respectivamente (, p. 19-20).

É interessante a ação de controle on/off ter um intervalo diferencial na referência para evitar comutações excessivas.

Falhou ao verificar gramática (função desconhecida '\begin{matrix}'): {\displaystyle u(t) =  \left \{ \begin{matrix} U_1, & \mbox{se  e(t) > 0} \\ U_2, & \mbox{se e(t) < 0} \end{matrix} \right }

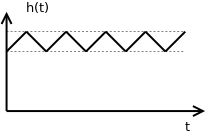
Gráfico da saída com controle On/Off

A saída de um sistema com controle On/Off oscila entre dois pontos, ligeiramente acima e abaixo da referência.

Controle Proporcional

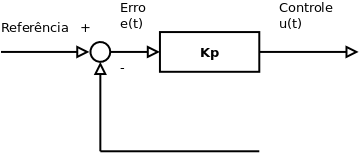
O controle proporcional ajusta a ação de controle de forma proporcional ao erro gerado (, p. 21).

$u(t)=K_{p}e(t)$

Função de Transferência (Transformada de Laplace):

${U_{s} \over E_{s}}=K_{p}$

A ação de controle proporcional funciona como um amplificador com ganho variável, proporcional ao erro.

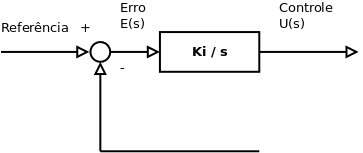
Controle Integral

O controle integral ajusta a ação de controle em função ao somatório do erro em um dado intervalo de tempo (, p. 21).

$u(t)=K_{i}\int _{0}^{t}e(t)dt$

Função de Transferência (Transformada de Laplace):

${U_{s} \over E_{s}}={K_{i} \over s}$

Ação de controle integral

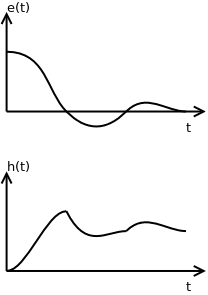
Na ação de controle integral a saída do controlador é igual a área sobre a curva do erro (integral do erro) atuante até aquele instante de tempo (, p. 197).

Quando o erro fica nulo a ação de controle permanece num estado estacionário, função do somatório dos erros anteriores.

Gráfico do Controle Integral:

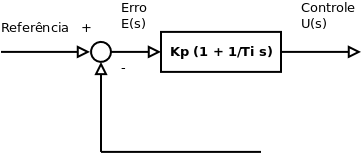
Controle Proporcional Integral

O controle proporcional integral combina a ação de controle proporcional e integral (, p. 21).

$u(t)=K_{p}e(t)+{K_{p} \over T_{i}}\int _{0}^{t}e(t)dt$

onde, T_i é o tempo integral.

Função de Transferência (Transformada de Laplace):

${U_{s} \over E_{s}}=K_{p}(1+{1 \over T_{i}s})$ 

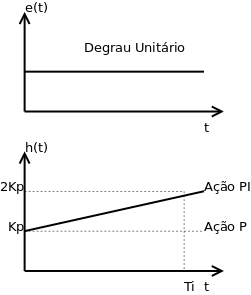
Erro estacionário do controle proporcional

Sem o controle integral há um erro estacionário (também chamado erro residual) inerente ao controle proporcional (, p. 197).

Gráfico do Controle PI:

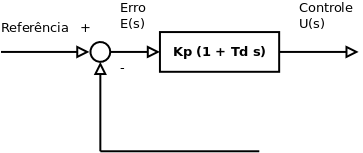
Controle Proporcional Derivativo

O controle proporcional derivativo combina o controle proporcional com o controle derivativo. O controle derivativo procura ajustar a ação de controle em função da taxa de variação do erro (, p. 21).

$u(t)=K_{p}e(t)+K_{p}T_{d}{de(t) \over dt}$

onde, T_d é o tempo derivativo.

Função de Transferência (Transformada de Laplace):

${U_{s} \over E_{s}}=K_{p}(1+T_{d}s)$

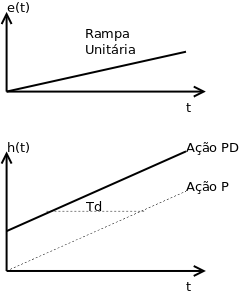
Ação do controle derivativo

A ação do controle derivativo é proporcional a taxa de variação do erro atuante. Deve ser usada em períodos transitórios (, p. 201).

Gráfico do Controle PD:

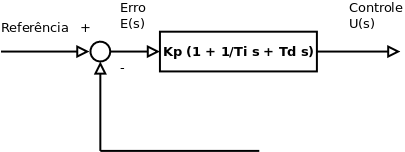
Controle Proporcional Integral Derivativo

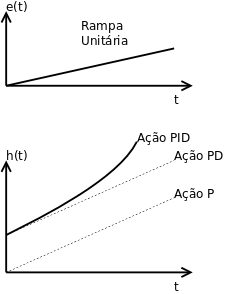
O controle proporcional integral derivativo combina as três ações de controle, visando atingir rapidamente a referência, minimizando os transitórios e eliminando o possível erro residual (, p. 21).

$u(t)=K_{p}e(t)+{K_{p} \over T_{i}}\int _{0}^{t}e(t)dt+K_{p}T_{d}{de(t) \over dt}$

onde, T_i é o tempo integral e T_d é o tempo derivativo.

Função de Transferência (Transformada de Laplace):

${U_{s} \over E_{s}}=K_{p}(1+{1 \over T_{i}s}+T_{d}s)$

Gráfico do Controle PID:

Referências

---

--Evandro.cantu (discussão) 19h03min de 4 de maio de 2018 (BRT)

---