Debounce

De Wiki Cursos IFPR Foz
Ir para navegaçãoIr para pesquisar

Bounce

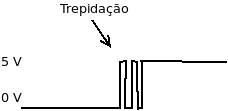
O termo bounce se refere a trepidações que podem ocorrer na abertura ou fechamento de chaves mecânicas em circuitos elétricos, gerando múltiplas transições na chave antes de estabilizar em um valor. Estas múltiplas transições, ou falsos acionamentos da chave, podem provocar funcionamento errôneo de dispositivos, como por exemplo, de um microcontrolador que esteja fazendo leituras do estado desta chave.

Chaves elétricas

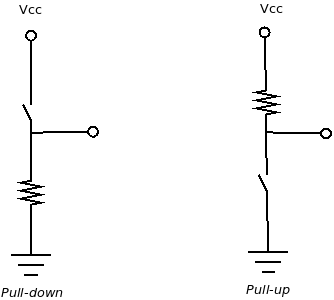
Uma chave elétrica simples geralmente envolve uma chave mecânica e um resistor. O resistor utilizado junto com a chave pode ser configurado como resistor pull-down ou resistor pull-up:

  • Pull-down se o resistor estiver conectado a terra;
  • Pull-up se o resistor estiver conectado ao Vcc.

  • Na configuração pull-down, quando a chave estiver aberta, o ponto de leitura tem nível baixo, por está conectado ao terra. Quando a chave for fechada o ponto de leitura parra a nível alto.
  • Na configuração pull-up, quando a chave estiver aberta, o ponto de leitura tem nível alto, por está conectado ao Vcc. Quando a chave for fechada o ponto de leitura parra a nível baixo.

Eliminação das trepidações ou debounce

O efeito bounce se refere a trepidações que podem ocorrer na abertura ou fechamento de chaves em circuitos elétricos, gerando múltiplas transições na chave antes de estabilizar em um valor.

Para eliminar o efeito das trepidações, ou debouce, pode-se utilizar técnicas de hardware, eliminando o as trepidações antes do microcontrolador fazer a leitura do dado, ou utilizar técnicas de software e utilizar algoritmos no microcontrolador para eliminar as trepidações indesejáveis após a leitura.

Eliminação das trepidações por hardware

Uma solução simples para eliminar as trepidações em chaves é baseada no uso de circuitos RC série, aproveitando a constante de tempo (τ) de carga e descarga do capacitor [1].

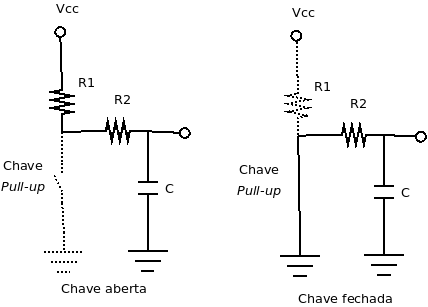
No circuito acima, R1 é o resistor pull-up conectado a chave. O resistor R2 e o capacitor C foram incluídos como uma rede RC para eliminar o efeito da trepidação da chave. Variações do circuito pode ser construídas para chaves conectadas a resistores pull-down.

Funcionamento do circuito

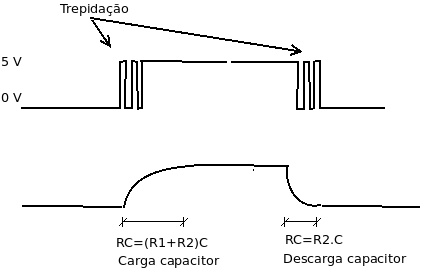
  1. Quando a chave estiver aberta o capacitor C vai ser carregado através dos resistores R1 e R2 e a constante de tempo será ((R1 + R2) * C).
  2. Quando a chave estiver fechada o capacitor C vai ser descarregado através do resistor R2 e a constante de tempo será (R2 * C).

Durante a trepidação da chave o capacitor não se descarrega/carrega totalmente devido a constante de tempo. Somente após a estabilização da chave o processo de carga e descarga do capacitor ficará consolidado.

Observe que a carga e descarga do capacitor eliminou as trepidações e fez com que a transição entre os níveis alto e baixo seguissem o formato exponencial da curva de carga e descarga do capacitor. Desta forma, há um atraso, ocasionado pela constante de tempo, para que o microcontrolador detecte cada transição da chave.

Note também que a constante de tempo de carga do capacitor é maior que a constante de tempo de descarga do capacitor.

Para a escolha correta dos resistores e capacitores deve garantir que o tempo de carga e descarga do capacitor seja superior ao tempo de estabilização da chave.

Observações
  1. Note também que o capacitor R2 poderia ser desnecessário quando a chave for aberta, pois neste caso o resistor R1 poderia controlar sozinho a carga do capacitor e eliminar as trepidações. Entretanto, quando a chave for fechada, caso o resistor R2 não existisse, o capacitor seria colocado em curto, descarregando instantaneamente, podendo provocar danos ou imprecisões no funcionamento do circuito. [2]
  2. Verifiquei algumas soluções que não utilizam o resistor R2 (como [3] e [4]), entretanto, pela dificuldade de entender o processo de descarga instantânea do capacitor, prefiro ficar com a solução acima.

Carga e descarga do capacitor com mesma constante de tempo

Um dos problemas do circuito acima é que a constante de tempo de carga do capacitor é maior que a constante de tempo de descarga do capacitor.

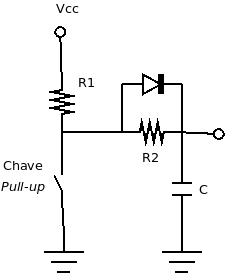
Uma solução para igualar as constante de tempo é utilizar um diodo em paralelo com o resistor R2, como mostra o circuito:

Funcionamento do circuito

Vamos assumir que a chave esteja inicialmente aberta e o capacitor esteja carregado:

  1. Quando a chave for fechada, o diodo ficará com polarização reversa (sem conduzir) e o capacitor vai se descarregar através de R2, com constante de tempo (R2*C).
  2. Quando a chave for novamente aberta, o capacitor vai estar inicialmente descarregado e o diodo estará com polarização direta (conduzindo), fazendo que a corrente que vai carregar o capacitor circule por R1 e pelo diodo, com constante de tempo (R1*C).

Assim, se escolhermos R1 = R2 as constantes de tempo de carga e descarga do capacitor serão iguais.

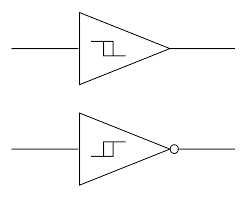
Smith Trigger

O circuito acima ainda tem um problema, que é o fato da transição da chave se dar de forma lenta, segundo a curva de carga e descarga do capacitor. Isto pode ser um problema para circuitos digitais, os quais necessitam identificar corretamente os níveis lógicos 0 (baixo) e 1 (alto).

Dependendo da tecnologia, os circuitos digitais podem trabalhar com tensões de 0V-5V (TTL) ou tensões 0V-3,3V (CMOS).

No Arduino Uno, que trabalha com 0V-5V, por exemplo, sinais abaixo de 1,5 V são considerados como nível lógico 0 e sinais acima de 3,0 V são considerados como nível lógico 1. Portanto, a transição lenta da chave, passando por valores indeterminados, pode causar imprecisões na interpretação dos sinais.

Uma solução para eliminar este problemas é utilizar dispositivos chamados Schmitt trigger.

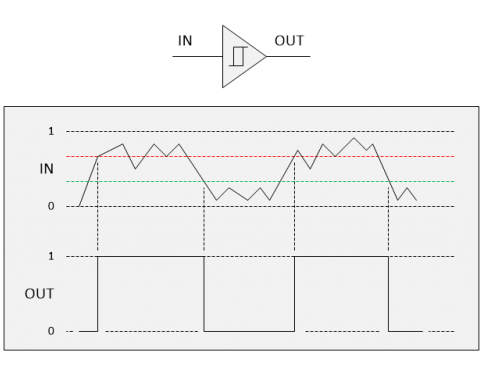
O Schmitt trigger tem dois limites para transição de estados, um mais alto para transição de 0 para 1, e outro mais baixo para transição de 1 para 0. Esta ação com dois limites de transição é chamada de histerese.

[1]

Na figura a transição de 0 para 1 ocorre somente quando o sinal de entrada ultrapassar a linha vermelha e a transição de 1 para 0 ocorre somente quando o sinal de entrada for a baixo da linha verde. Desta forma, se pode eliminar valores intermediários que possam causar indeterminações quando aos níveis lógicos 0 e 1.

Referências

  1. ↑ 1,0 1,1 Max Maxfield. Ultimate Guide to Switch Debounce, 2020. https://www.eejournal.com/article/ultimate-guide-to-switch-debounce-part-3/
  2. ↑ http://www.ganssle.com/debouncing-pt2.htm
  3. ↑ https://www.embarcados.com.br/leitura-de-chaves-debounce/
  4. ↑ https://eletronworld. com.br/eletronica/efeito-bounce/

Evandro.cantu (discussão) 17h50min de 23 de setembro de 2021 (-03)

Disponível em “http://wiki.foz.ifpr.edu.br/wiki/index.php?title=Debounce&oldid=28496”