Laboratorio M1K Analog Devices: Filtros Eletricos
Laboratório: Introdução aos filtros elétricos
Este laboratório foi baseado no material disponibilizado pela Analog Devices, fabricante do módulo educacional M1K Analog Devices: [1]
Objetivos
Conhecer o princípio de funcionamento dos filtros elétricos RC passa baixa e passa alta.
Construir circuitos detectores de pico, com diodos e capacitores, visando detectar a máxima amplitude do sinal de saída de um filtro elétrico.
Equipamento e Materiais
- Modulo Analog Devices M1K e software Pixelpulse
- Componentes Eletrônicos:
- Resistores: 68Ω,100Ω 10KΩ, 200KΩ
- Capacitores: 10uF, 22uF e 47uF
- Leds
- Diodo 1N914
- Circuito Integrado AD8561
Procedimentos Práticos
Filtro passa baixa
- Identifique os resistores e capacitores a serem utilizados no experimento. Observe que os capacitores eletrolíticos tem polaridade, portanto, devem ser montados no circuito considerando os terminais positivo e negativo.
- Monte na matriz de contatos o filtro RC da figura, usando o resistor de 68Ω e o capacitor de 22uF:
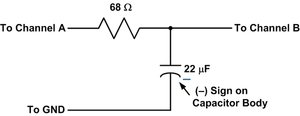 [1]
[1] - Selecione o canal A do módulo Analog Devices M1K para Gerar Tensão/Medir Corrente e o canal B para Medir Voltagem.
- Configure o canal A para gerar uma onda senoidal com 10 Hz de frequência e tensão variando de 0 V a 5 V. Observe no canal B a forma de onda sobre o capacitor.
- Gradualmente aumente a frequência da onda senoidal até 1000 Hz e observe no canal B a redução da amplitude da forma de onda sobre o capacitor.
- Ajuste a frequência da onda senoidal no canal A até que a amplitude da onda no canal B seja 3,5 V.
Filtro passa alta
- Monte na matriz de contatos o filtro RC da figura, usando o resistor de 68Ω e o capacitor de 10F:
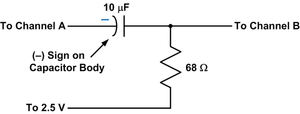 [1]
[1] - Configure o canal A para gerar uma onda senoidal com 10 Hz de frequência e tensão variando de 0 V a 5 V. Observe no canal B a forma de onda sobre o capacitor.
- Gradualmente aumente a frequência da onda senoidal até 1000 Hz e observe no canal B a redução da amplitude da forma de onda sobre o capacitor.
- Ajuste a frequência da onda senoidal no canal A até que a amplitude da onda no canal B seja 3,5 V.
Fundamentos sobre Filtros Elétricos
Filtros elétricos são circuitos que permitem filtrar determinadas frequências de um sinal CA permitindo a passagem de algumas frequências e limitando a passagem de outras. A frequência de transição entre as frequências permitidas e as não permitidas é chamada frequência de corte (fc).
Um filtro que permite a passagem de frequências abaixo da frequência de corte é chamado de filtro passa baixas e um filtro que permite a passagem de frequências a acima frequência de corte é chamado de filtro passa altas.
Os filtros elétricos mais simples podem ser construídos com elementos passivos, como resistores e capacitores (filtros RC) ou resistores e indutores (filtros RL).
Filtros RC
Com circuitos RC série é possível construir filtros elétricos passa baixas e passa altas. Os filtros operam sobre o divisor de tensão entre o resistor (R) e a reatância do capacitor (C).
A reatância é a oposição a passagem de corrente elétrica de capacitores e indutores em circuitos de corrente alternada. A reatância é um parâmetro que depende da frequência do sinal de corrente alternada.
Para um capacitor a reatância é dada por 1/2πfC. Pela expressão pode-se ver que a reatância capacitiva varia inversamente proporcional a frequência, ou seja, se a frequência aumenta a reatância diminui e vice versa. Para corrente contínua (frequência zero) a reatância capacitiva tende ao infinito, ou seja, o capacitor se comporta como um circuito aberto.
A
Series RC circuits can realize the simplest lowpass and highpass filters that operate on voltages, though current-mode operation is also possible. The filter is lowpass when the output voltage is taken across the capacitor and is highpass when the output voltage is taken across the resistor. The filter operates as a two-element voltage divider between the resistance of the resistor, R, and the reactance of the capacitor, 1/2πfC. Since the capacitive reactance varies inversely with frequency, the voltage across the capacitor decreases with frequency, producing the lowpass frequency response. By Kirchhoff's Voltage Law, the voltage across the resistor increases with frequency in a complementary fashion to that of the capacitor, producing the highpass response. The cutoff frequency fC is defined as the frequency at which the capacitive reactance is equal to the resistance. Setting R = 1/2πfCC and solving for fC gives the following result.
f_C = 1/{2 pi RC}
Observações e Conclusões
- '
Referências
Evandro.cantu (discussão) 10h03min de 13 de julho de 2020 (-03)