Árvores

Árvores

Uma árvore binária é uma estrutura de dados formada por um conjunto finito de elementos ou nós. Uma árvore pode esta vazia ou formada por um nó chamado raiz e dois sub-conjuntos de elementos chamados sub-árvore esquerda e sub-árvore direita. As sub-árvore esquerda e sub-árvore direita são também árvores binárias e podem estar vazias .

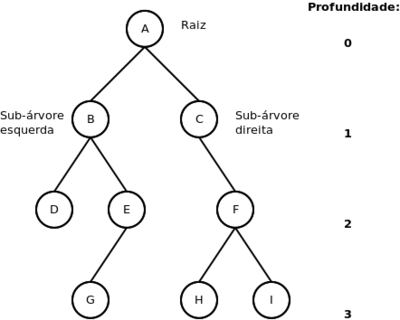
A figura ilustra uma árvore binária :

Na figura:

• O nó raiz A tem duas sub-árvores B e C;
• O nó B tem duas sub-árvores D e E;
• O nó C tem apenas a sub-árvore da direita F;
• O nó E tem apenas a sub-árvore da esquerda G;
• O nó F tem duas sub-árvores H e I;
• Os nós D, G, H e I não tem sub-árvores, portanto, são chamados folhas.

Se A tem duas sub-árvores B e C, diz-se que:

• A é pai de B e C;
• B é filho esquerdo de A;
• C é filho direito de A.
• B é irmão de C.

Profundidade da árvore binária

Numa árvore binária, o nó raiz é considerado como profundidade 0 (zero). As sub-árvores do nó raiz profundidade 1, e assim sucessivamente. No exemplo da figura, a árvore binária tem profundidade 3.

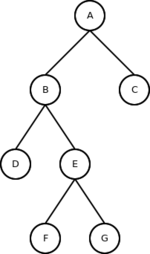
Árvore estritamente binária

Uma árvore é estritamente binária se todo nó que não for folha tenha as sub-árvores direita e esquerda não vazias.

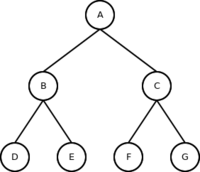
Árvore binária completa

Uma árvore é binária completa se for uma árvore estritamente binária e todas as folhas estiverem na mesma profundidade.

Aplicações das árvores binárias

As árvores binárias são uma estrutura de dados útil quando precisam ser tomadas decisões bi-direcionais em cada ponto do processo. Por exemplo, suponha que queiramos encontrar repetições em uma lista de números. Uma maneira de fazer isto é comparar cada número com todos os que o precedem. Entretanto, isto pode envolver muitas comparações. Outra maneira é utilizar uma árvore binária .

Exemplo

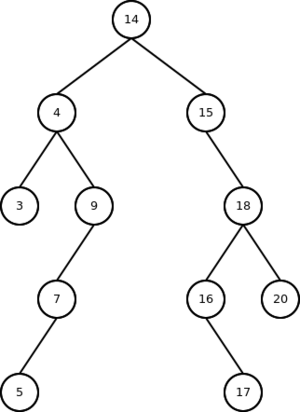
Suponha que temos a seguinte lista de números para verificar repetições:

14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Neste caso, iniciamos a árvore com o primeiro número da lista como sendo o nó raiz. Na sequência, comparamos o próximo número com o número da raiz, se for igual é uma repetição. Se for menor, comparamos com a sub-árvore da esquerda. Se for maior, comparamos com a sub-árvore da direita. Se a sub-árvore estiver vazia, incluímos o número como filho desta sub-árvore, caso seja menor ou maior, da mesma forma que foi realizado no início.

Veja a árvore que seria construída neste exemplo:

Percorrendo uma árvore

Uma operação importante em uma árvore binária é percorrer todos os seus nós.

Diferentemente de uma lista, na qual os nós são percorridos de maneira linear, numa árvore, existem diferentes ordens para poder percorrê-la.

Um método bastante comum para percorrer uma árvore é a ordem esquerda-raiz-direita .

Ordem esquerda-raiz-direita

Nesta ordem, percorre-se primeiro a sub-árvore esquerda, na ordem esquerda-raiz-direita. Depois a raiz. E depois a sub-árvore direita, também na ordem esquerda-raiz-direita.

Exemplo de ordem de varredura esquerda-raiz-direita:

      5
     / \
    3   8
   /   / \
  1   6   9
 / \   \
0   2   7

Referências

---

--Evandro.cantu (discussão) 09h43min de 11 de novembro de 2014 (BRST)

---