Sistemas de Controle: mudanças entre as edições
De Wiki Cursos IFPR Foz
Ir para navegaçãoIr para pesquisar
| Linha 19: | Linha 19: | ||
Função de Transferência: | Função de Transferência: | ||
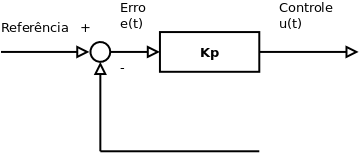
<math>{U_s \over E_s} = K_p </math> | <math>{U_s \over E_s} = K_p </math> (Transformada de Laplace) | ||
==Controle Integral== | ==Controle Integral== | ||
| Linha 29: | Linha 29: | ||
Função de Transferência: | Função de Transferência: | ||
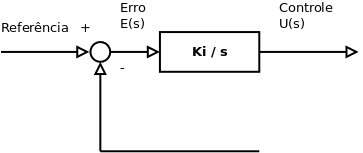
<math>{U_s \over E_s} = {K_i \over s} </math> | <math>{U_s \over E_s} = {K_i \over s} </math> (Transformada de Laplace) | ||
==Controle Proporcional Integral== | ==Controle Proporcional Integral== | ||
[[Arquivo:ControlePI.png]] | [[Arquivo:ControlePI.png]] | ||
<math>u(t) = K_p e(t) + {K_p \over T_i} \int_{0}^{t} e(t), dt </math> | |||
Função de Transferência: | |||
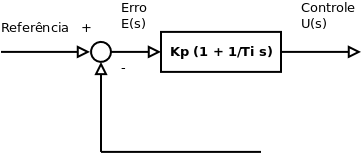
<math>{U_s \over E_s} = K_p ({1 + 1 \over T_i s}) </math> (Transformada de Laplace) | |||
==Controle Proporcional Derivativo== | ==Controle Proporcional Derivativo== | ||
Edição das 22h28min de 4 de maio de 2018
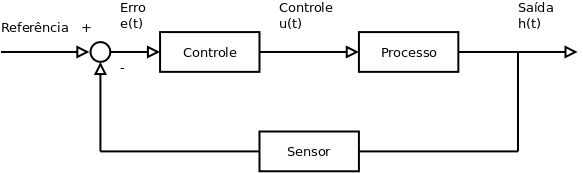
Sistemas de Controle
Referências: [1].
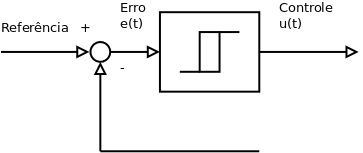
Controle On / Off
Falhou ao verificar gramática (função desconhecida '\begin{matrix}'): {\displaystyle u(t) = \left \{ \begin{matrix} U_1, & \mbox{se e(t) > 0} \\ U_2, & \mbox{se e(t) < 0} \end{matrix} \right. }
Controle Proporcional
Função de Transferência:
(Transformada de Laplace)
Controle Integral
Função de Transferência:
(Transformada de Laplace)
Controle Proporcional Integral
Função de Transferência:
(Transformada de Laplace)
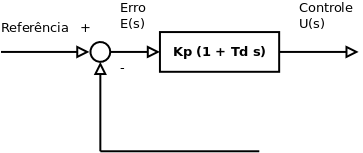
Controle Proporcional Derivativo
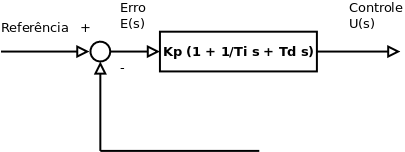
Controle Proporcional Integral Derivativo
Referências
Referências
- ↑ OGATA, Katsuhiko. Engenharia de Controle Moderno, LTC, 2011.
--Evandro.cantu (discussão) 19h03min de 4 de maio de 2018 (BRT)