Logica Binaria

Lógica Binária

A lógica binária é a base de todo o cálculo computacional. Na verdade, são estas operações mais básicas que constituem todo o poderio dos computadores. Qualquer operação, por mais complexa que pareça, é traduzida internamente pelo processador para estas operações.

Portas Lógicas

As portas lógicas implementam os operadores da lógica binária e são os principais componentes da eletrônica digital.

Portas lógicas na Wikipédia

Representação elétrica dos bits 0 e 1

Uma forma típica de representar os bits 0 e 1 nos sistemas eletrônicos a através de níveis de tensão elétrica. Nos circuitos integrados (CI) TTL (transistor transistor logic) utiliza-se os níveis de tensão 0V (nível BAIXO) para representar o 0 e 5V (nível ALTO) para representar 1. Outras tecnologias de CI, como a CMOS, utilizam outros níveis de tensão.

Porta NÃO (NOT)

Implementa o operador NÃO (NOT), ou negação binária, resulta no complemento do operando, ou seja, será um bit 1 se o operando for 0, e será 0 caso contrário, conforme podemos confirmar pela tabela verdade, onde A é o bit de entrada e S é o bit de saída (out):

A	S
0	1
1	0

Expressão booleana:

S = /A

Porta Não na Wikipédia

Porta E (AND)

Implementa o operador E (AND), ou conjunção binária, devolve um bit 1 sempre que ambos operandos sejam 1, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):

A	B	S
0	0	0
0	1	0
1	0	0
1	1	1

Expressão booleana:

S = A . B

Porta E na Wikipédia

Porta OU (OR)

Implementa o operador OU (OR), ou disjunção binária, devolve um bit 1 sempre que pelo menos um dos operandos seja 1, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):

A	B	S
0	0	0
0	1	1
1	0	1
1	1	1

Expressão booleana:

S = A + B

Porta OU na Wikipédia

Portas Não E (NAND) e Não OU (NOR)

Correspondem aos operadores E e OU, seguidos por uma negação, respectivamente.

Expressões booleanas:

• Não E

S = /(A . B)

• Não OU

S = /(A + B)

Porta OU-EXCLUSIVO (XOR)

Implementa o operador OU-EXCLUSIVO (XOR), ou disjunção binária exclusiva, devolve um bit 1 sempre que o número de operandos iguais a 1 é ímpar, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):

A	B	S
0	0	0
0	1	1
1	0	1
1	1	0

Exercícios

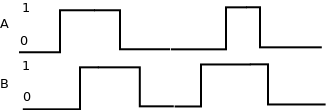
1. Determine a saída da porta OU considerando que as entradas A e B variam de acordo com o diagrama de tempo mostrado.
   • 
2. Determine a saída da porta E considerando que as entradas A e B variam de acordo com o diagrama de tempo mostrado.
   • 

Descrevendo circuitos lógicos algebricamente

Qualquer circuito lógico pode ser descrito usando os três operadores lógicos fundamentais: E, OU e NÃO.

Por exemplo, se tivermos um circuito descrito por S = A . B . C, sabemos que trata-se de uma porta E de três entradas. Se tivermos um circuito descrito por S = A + /B, sabemos que trata-se de uma porta OU com a entrada B invertida.

Exemplo

Circuito construído a partir da expressão lógica:

S = (A + B).(/B + C)

Note que:

• As expressões (A + B) e (/B + C) são entradas de uma porta E;
• A expressão A + B é gerada por portas OU;
• A expressão /B + C tambḿ é gerada por portas OU, com um inversor na entrada B.

Exercício

1. Construa a tabela verdade para o circuito apresentado no exemplo anterior: S = (A + B).(/B + C).
2. Construa o circuito gerado pela expressão S = A.C + /(B.C) + /A.B.C
3. Construa a tabela verdade para o circuito do exercício anterior.

Álgebra de Boole

Álgebra de Boole na Wikipédia

Teoremas Booleanos

1. A . 0 = 0
2. A . 1 = A
3. A . A = A
4. A . /A = 0
5. A + 0 = A
6. A + 1 = 1
7. A + A = A
8. A + /A = 1

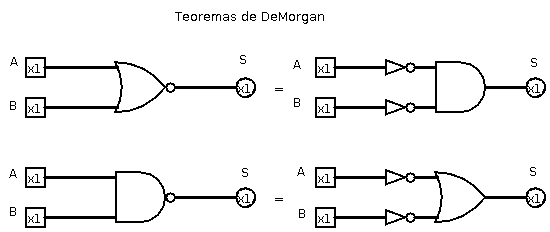
Teoremas de DeMorgan

• /(A + B) = /A . /B
• /(A . B) = /A + /A

Circuitos Combinacionais

Circuitos combinacionais são circuitos cujo nível lógico da(s) saída(s) depende da combinação dos níveis lógicos das entradas.

Um circuito lógico não possui característica de memória de estados anteriores, dependendo sempre apenas dos valores atuais das entradas.

Laboratório de simulação de circuitos combinacionais

Vamos utilizar o software disponível em http://www.falstad.com/mathphysics.html para simular o funcionamento de alguns Ciruitos Lógicos Combinacionais (Combinational Logic).

Ou-Exclusivo (XOR)

Testar a tabela verdade do circuito Ou-Exclusivo (XOR). Note que o circuito Ou-Exclusivo é construído a partir de portas NÂO-E (NAND). Acompanhar os valores 1 e 0 nas entradas, saídas e também nos pontos internos do circuito.

Meio Somador (Half Adder)

Testar o circuito Meio Somador (Half Adder). O circuito tem duas entradas com os bits a serem somados e duas saídas, uma com a soma e outra com o carry (vai um). Construir a tabela verdade do circuito.

Somador Completo (Full Adder)

Testar o circuito Somador Completo (Full Adder). O circuito tem três entradas, incluindo os dois bits a serem somados e o carry da coluna anterior e duas saídas, uma com a soma e outra com o carry (vai um) para a próxima coluna. Construir a tabela verdade do circuito.

Exercício

Desenhar um circuito somador de dois bits a partir da integração de um meio somador e um somador completo.

---