Logica Binaria: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 30: | Linha 30: | ||
|- | |- | ||
|} | |} | ||
Expressão booleana: | |||
S = /A | |||
[http://pt.wikipedia.org/wiki/Porta_NOT Porta Não na Wikipédia] | [http://pt.wikipedia.org/wiki/Porta_NOT Porta Não na Wikipédia] | ||
| Linha 52: | Linha 55: | ||
|- | |- | ||
|} | |} | ||
Expressão booleana: | |||
S = A . B | |||
[http://pt.wikipedia.org/wiki/Porta_AND Porta E na Wikipédia] | [http://pt.wikipedia.org/wiki/Porta_AND Porta E na Wikipédia] | ||
| Linha 74: | Linha 80: | ||
|- | |- | ||
|} | |} | ||
Expressão booleana: | |||
S = A + B | |||
[http://pt.wikipedia.org/wiki/Porta_OR Porta OU na Wikipédia] | [http://pt.wikipedia.org/wiki/Porta_OR Porta OU na Wikipédia] | ||
| Linha 80: | Linha 89: | ||
Correspondem aos operadores E e OU, seguidos por uma negação, respectivamente. | Correspondem aos operadores E e OU, seguidos por uma negação, respectivamente. | ||
Expressões booleanas: | |||
*Não E | |||
S = /(A . B) | |||
*Não OU | |||
S = /(A + B) | |||
====Porta OU-EXCLUSIVO (XOR)==== | ====Porta OU-EXCLUSIVO (XOR)==== | ||
Edição das 19h29min de 24 de março de 2014
Lógica Binária
A lógica binária é a base de todo o cálculo computacional. Na verdade, são estas operações mais básicas que constituem todo o poderio dos computadores. Qualquer operação, por mais complexa que pareça, é traduzida internamente pelo processador para estas operações.
Portas Lógicas
As portas lógicas implementam os operadores da lógica binária e são os principais componentes da eletrônica digital.
Representação elétrica dos bits 0 e 1
Uma forma típica de representar os bits 0 e 1 nos sistemas eletrônicos a através de níveis de tensão elétrica. Nos circuitos integrados (CI) TTL (transistor transistor logic) utiliza-se os níveis de tensão 0V (nível BAIXO) para representar o 0 e 5V (nível ALTO) para representar 1. Outras tecnologias de CI, como a CMOS, utilizam outros níveis de tensão.
Porta NÃO (NOT)
Implementa o operador NÃO (NOT), ou negação binária, resulta no complemento do operando, ou seja, será um bit 1 se o operando for 0, e será 0 caso contrário, conforme podemos confirmar pela tabela verdade, onde A é o bit de entrada e S é o bit de saída (out):
| A | S |
| 0 | 1 |
| 1 | 0 |
Expressão booleana:
S = /A
Porta E (AND)
Implementa o operador E (AND), ou conjunção binária, devolve um bit 1 sempre que ambos operandos sejam 1, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Expressão booleana:
S = A . B
Porta OU (OR)
Implementa o operador OU (OR), ou disjunção binária, devolve um bit 1 sempre que pelo menos um dos operandos seja 1, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Expressão booleana:
S = A + B
Portas Não E (NAND) e Não OU (NOR)
Correspondem aos operadores E e OU, seguidos por uma negação, respectivamente.
Expressões booleanas:
- Não E
S = /(A . B)
- Não OU
S = /(A + B)
Porta OU-EXCLUSIVO (XOR)
Implementa o operador OU-EXCLUSIVO (XOR), ou disjunção binária exclusiva, devolve um bit 1 sempre que o número de operandos iguais a 1 é ímpar, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Exercícios
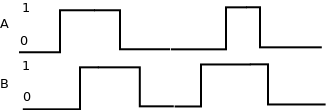
- Determine a saída da porta OU considerando que as entradas A e B variam de acordo com o diagrama de tempo mostrado.
- Determine a saída da porta E considerando que as entradas A e B variam de acordo com o diagrama de tempo mostrado.