TADS:Introdução a Computação: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 95: | Linha 95: | ||
== 24/fev == | == 24/fev == | ||
===Sistemas Numéricos=== | ===Sistemas Numéricos=== | ||
| Linha 281: | Linha 278: | ||
== 25/fev == | == 25/fev == | ||
* Apresentação e discussão dos programas desenvolvidos no Scratch. | |||
---- | |||
====Resumo Sistema Binário==== | ====Resumo Sistema Binário==== | ||
* Exemplo de binário de 8 bits: 10111100 | * Exemplo de binário de 8 bits: 10111100 | ||
Edição das 21h45min de 25 de fevereiro de 2014
INF 101 - Introdução a Computação
Carga Horária
60 horas -> 72 aulas (48 teóricas + 24 práticas)
Objetivos
Fornecer subsídios para o aluno conhecer e compreender os conceitos básicos da área de informática, computação e redes de computadores.
Ementa
- As novas tecnologias da informação e comunicação na sociedade contemporânea.
- O computador e a internet como ferramentas de trabalho e desenvolvimento para o profissional de informática.
- Histórico dos computadores e das redes de computadores.
- Informação digital e sua representação: códigos digitais, sistemas numéricos e aritmética computacional.
- Arquitetura e componentes básicos do hardware computador.
- Elementos da lógica digital: portas lógicas, flip-flops e suas aplicações.
- Memória do computador.
- Estrutura e funções do processador.
- Dispositivos de entrada e saída do computador.
- Interfaces e transmissão de dados serial e paralela.
- O software do computador: sistemas operacionais e aplicações.
- Linguagens de programação e sistemas de desenvolvimento de software.
- Fundamentos das redes de computadores e da Internet.
- Convergência das redes e aplicações multimídia.
Bibliografia Básica
- BROOKSHEAR, J. G. Ciência da Computação. 7 ed. São Paulo: Bookman, 2005.
- MOKARZEL, F.; SOMA, N. Y. Introdução a Ciência Da Computação. Elsevier, 2008
- MONTEIRO, Mário A.. Introdução à Organização de Computadores. 5. ed. Rio de Janeiro: LTC, 2012.
- FONCECA FILHO, C. História da computação: O Caminho do Pensamento e da Tecnologia. Porto Alegre: Edipucrs, 2007.
- KUROSE, J. F., ROSS, K., Redes de Computadores e a Internet: Uma Abordagem Top-down, 5ª ed, Addison Wesley, 2010.
Bibliografia Complamentar
- SCHIAVONI, Marilene. Hardware. Curitiba: Livro Técnico, 2010.
- VIEIRA, N. J. Introdução aos Fundamentos da Computação, Pioneira Thomson, 2006.
- VELOSO, F. C. Informática: Conceitos Básicos, 8 ed. Rio de Janeiro: Campus, 2011.
- TANEMBAUM, A. S. Organização Estruturada de Computadores. 5 ed. Rio de Janeiro: Prentice-Hall, 2006.
- STALLINGS, W. Arquitetura e Organização de Computadores. 8 ed. São Paulo: Pearson, 2010.
Materiais de Apoio
Semestre 2014-1
Professor: Evandro Cantú (evandro.cantu@ifpr.edu.br)
Encontros: 2a feira / 3a feira - 19h-20h40 - 4 aulas/semana
Atendimento paralelo: 2a feira / 3a feira - 18h-18h50.
Pasta Compartilhada GoogleDrive: https://drive.google.com/folderview?id=0B4oNxt3g19DfbzlXSWVVbE51V0k&usp=sharing
Grupo de Email da turma: tads-ifprfoz@googlegroups.com
Diários de Aula
10/fev
Introdução aos Computadores e a Informática
- Conceitos sobre computadores
- Vídeos sugeridos: Bits e Bytes: que mundo é este
- Textos sugeridos para leitura:
11/fev
Debate sobre textos discutindo o futuro da informática:
- Síntese: Futuro da Internet
- Síntese: Próximos 10 anos
- Tarefa para casa: Produzir texto descrevendo suas experiências e expectativas profissionais com a área de informática (Entregar em 18/fev)
Conceitos Computadores e a Informática
- Assistimos vídeo: Bits e Bytes: Que mundo é este - Parte 2
- Hardware do computador
- Bits e Bytes
- Números binários de base 2
- Prefixos do Sistema Internacional (SI) X Prefixos Binários
17/fev
Não haverá aulas de Introdução a Computação -> Quatro aulas de Lógica de Programação (Marcela)
18/fev
Não haverá aulas de Lógica de Programação -> Quatro aulas de Introdução a Computação (Evandro)
Como escolher um computador:
- Hardware do computador
- Performance de um computador -> Velocidade do processador, Memória RAM, Placa Mãe
- Performance do processador -> Frequência do clock, Largura dos registradores em bits, Memória Cache, Múltiplos Núcleos
- Velocidade de transmissão de bits (bps)
- Tarefa para aula: Realizar uma escolha fictícia de um computador para comprar, justificando a escolha em termos de qual uso pretende fazer, preço e performance da máquina.
24/fev
Sistemas Numéricos
Sistema Decimal:
- Base: 10
- Digitos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Exemplo: 5374 = 5 x 103 + 3 x 102 + 7 x 101 + 4 x 100
Sistema Binário:
- Base: 2
- Digitos: 0, 1
- Exemplo: 1100 = 1 x 23 + 1 x 22 + 0 x 21 + 0 x 20 -> 8 + 4 + 0 + 0 = 12
Vídeo: Sistema binário
| Bits | Combinações | Binários |
|---|---|---|
| 1 | 21 = 2 | 0
1 |
| 2 | 22 = 4 | 00
01 10 11 |
| 3 | 23 = 8 | 000
001 010 011 100 101 110 111 |
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024 -> 1 Kibi bit Prefixos Binários
Sistema Octsal:
- Base: 8
- Digitos: 0, 1, 2, 3, 4, 5, 6, 7
- Correspondência entre binário de 3 bits e octal:
| Decimal | Binário | Octal |
|---|---|---|
| 0 | 000 | 0 |
| 1 | 001 | 1 |
| 2 | 010 | 2 |
| 3 | 011 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
Sistema Hexadecimal:
- Base: 16
- Digitos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
- Correspondência entre binário de 4 bits e hexadecimal:
| Decimal | Binário | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
- Contagem em Hexadecimal:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F,
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F,
20, ... 2F,
30, ... 3F,
...
90, ... 9F,
A0, ... AF,
B0, ... BF,
...
F0, ... FF,
100, ..., 10F,
...
Conversão de Bases:
- Binário -> Decimal
- Para converter de binário para decimal, soma-se os pesos das posições em que o número binário tiver um bit 1.
- Exemplos:
- 101101 = 1 x 25 + 1 x 23 + 1 x 22 + 1 x 20 = 32 + 8 + 4 + 1 = 45
- 10100011 = 128 + 32 + 2 + 1 = 163
- Decimal -> Binário
- Uma das maneiras de converter um número decimal em binário e realizar divisões sucessivas por 2.
- Exemplo:
- 25/2 = 12 + resto 1
- 12/2 = 6 + resto 0
- 6/2 = 3 + resto 0
- 3/2 = 1 + resto 1
- 1/2 = 0 + resto 1
- -> 11001 (O bit mais significativo (MSB) é o último resto)
- Outra maneira de converter um número decimal em binário é expressar o decimal como soma de potências de 2 (processo inverso a conversão de binário para decimal).
- Binário <-> Hexadecimal
- Cada digito hexa é convertido no equivalente binário de 4 bits (conforme tabela), e vice-versa, cada quatro bits binários é convertido no hexa equivalente.
- Exemplos: Hexa -> Binário
- A3 = 1010 0011
- 7E = 0111 1110
- Exemplos: Binário -> Hexa
- 110110 = 0011 0110 = 36 (zeros são acrescentados a esquerda para formar grupos de 4 bits)
- 11000101 = 1100 0101 = C5
25/fev
- Apresentação e discussão dos programas desenvolvidos no Scratch.
Resumo Sistema Binário
- Exemplo de binário de 8 bits: 10111100
| Valores posicionais | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Potências de 2 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Exemplo binário | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| MSB | LSB |
- MSB: Bit mais significativo (most significant bit)
- LSB: Bit menos significativo (less significant bit)
Resumo sobre conversões de base:
- Quando converter binário em decimal, use o método da soma dos pesos de cada digito;
- Quando converter decimal em binário, use o método de divisões sucessivas por 2, reunindo os restos da divisão;
- Quando converter binário em hexa, agrupe os bits em grupo de quatro e converta cada grupo no hexa equivalente;
- Quando converter hexa em binário, converta cada digito em 4 bits equivalentes.
Exercícios:
- Converter o binário 1000110110112 em decimal;
- Qual o peso do MSB (Bit mais significativo) de um número de 16 bits?
- Qual a faixa total de valores decimais que podemos representar com 8 bits?
- Quantos bits são necessários para representar valores decimais de 0 a 12.500?
- Converter o decimal 72910 em binário;
- Converter o decimal 37810 em um número binário de 16 bits e depois também em hexadecimal;
- Converter o hexadecimal B2F16 em um número binário e depois também em decimal;
- Converter o decimal 42310 em hexa;
- Converter o decimal 21410 em hexa.
Outros códigos binários utilizados na informática e eletrônica digital
Código BCD
Vimos que um número digital pode ser representado por um binário equivalente, por exemplo, o decimal 1310 pode ser representado pelo binário 11012. Isto é chamado codificação em binário puro.
Em alguns casos é interessante representar cada digito decimal pelo seu binário equivalente, o resultado será um código denominado decimal codificado em binário (BCD - binary coded decimal).
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| BCD | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
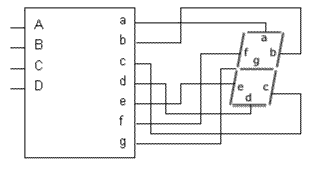
Um dos usos do código BCD é quando precisamos enviar cada digito digital para ser mostrado em um display de 7 segmentos, utilizando um CI chamado conversor BCD para 7 segmentos:
Código Gray
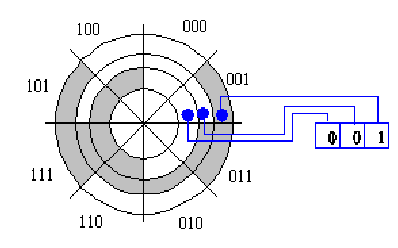
O código Gray permite representar sequências de números de forma que apenas um bit muda entre dois números sucessivos.
Exemplo de aplicação em leitor binário de posição de 3 bits;
Código ASCII
O código ASCII é um código alfanumérico, utilizado como padrão para a troca de informações entre a CPU de um computador e dispositivos como teclado, moditores e impressoras, por exemplo.
No código ASCII cada caractere é codificado em 7 bits, existindo, portanto, 27 = 128 representações codificadas.
Exercícios:
- Codifique os números decimais a seguir em BCD:
- 47,
- 962,
- 6727;
- Quantos bits são necessários para representar os números decimais na faixa de 0 a 999 usando:
- Binário puro;
- BCD.
- Represente a expressão entre aspas "X = 3 x Y" em código ASCII.
- Os Bytes a seguir (mostrados em hexa) representam o nome de uma pessoa am ASCII, com um bit MSB anexado. Determine o nome da pessoa:
- 42 45 4E 20 53 4D 49 54 48