Logica Binaria

Lógica Binária

A lógica binária é a base de todo o processamento computacional. Na verdade, são estas operações mais básicas que constituem todo o poderio dos computadores. Qualquer operação, por mais complexa que pareça, é traduzida internamente pelo processador para operações lógicas, realizadas por meio de portas lógicas.

Representação elétrica dos bits 0 e 1

Uma forma típica de representar os bits 0 e 1 nos sistemas eletrônicos a através de níveis de tensão elétrica.

Nos circuitos integrados (CI) TTL (transistor transistor logic) utiliza-se os seguintes níveis de tensão:

• 0V (nível BAIXO) para representar o 0;
• 5V (nível ALTO) para representar 1.

Outras tecnologias de CI, como a CMOS, utilizam outros níveis de tensão.

Portas Lógicas

As portas lógicas implementam os operadores da lógica binária e são os principais componentes da eletrônica digital.

Portas lógicas na Wikipédia

Porta NÃO (NOT)

Implementa o operador NÃO (NOT), ou negação binária, resulta no complemento do operando, ou seja, será um bit 1 se o operando for 0, e será 0 caso contrário, conforme podemos confirmar pela tabela verdade, onde A é o bit de entrada e S é o bit de saída (out):

A	S
0	1
1	0

Expressão booleana:

S = /A

Porta E (AND)

Implementa o operador E (AND), ou conjunção binária, devolve um bit 1 sempre que ambos operandos sejam 1, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):

A	B	S
0	0	0
0	1	0
1	0	0
1	1	1

Expressão booleana:

S = A . B

Porta OU (OR)

Implementa o operador OU (OR), ou disjunção binária, devolve um bit 1 sempre que pelo menos um dos operandos seja 1, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):

A	B	S
0	0	0
0	1	1
1	0	1
1	1	1

Expressão booleana:

S = A + B

Portas Não E (NAND) e Não OU (NOR)

Correspondem aos operadores E e OU, seguidos por uma negação, respectivamente.

Expressões booleanas:

• Não E

S = /(A . B)

• Não OU

S = /(A + B)

Porta OU-EXCLUSIVO (XOR)

Implementa o operador OU-EXCLUSIVO (XOR), ou disjunção binária exclusiva, devolve um bit 1 sempre que o número de operandos iguais a 1 é ímpar, conforme podemos confirmar pela tabela verdade, onde A e B são bits de entrada e S é o bit de saída (out):

A	B	S
0	0	0
0	1	1
1	0	1
1	1	0

Exercícios

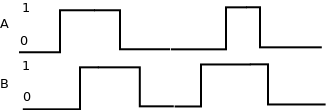
1. Determine a saída da porta OU considerando que as entradas A e B variam de acordo com o diagrama de tempo mostrado.
   • 
2. Determine a saída da porta E considerando que as entradas A e B variam de acordo com o diagrama de tempo mostrado.
   • 

Descrevendo circuitos lógicos algebricamente

Qualquer circuito lógico pode ser descrito usando os três operadores lógicos fundamentais: E, OU e NÃO.

Por exemplo, se tivermos um circuito descrito por S = A . B . C, sabemos que trata-se de uma porta E de três entradas. Se tivermos um circuito descrito por S = A + /B, sabemos que trata-se de uma porta OU com a entrada B invertida.

Exemplo

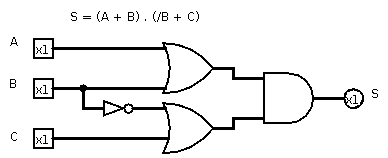
Circuito construído a partir da expressão lógica:

S = (A + B).(/B + C)

Note que:

• As expressões (A + B) e (/B + C) são entradas de uma porta E;
• A expressão A + B é gerada por portas OU;
• A expressão /B + C tambḿ é gerada por portas OU, com um inversor na entrada B.

Exercício

1. Construa a tabela verdade para o circuito apresentado no exemplo anterior: S = (A + B).(/B + C).
2. Construa o circuito gerado pela expressão S = A.C + /(B.C) + /A.B.C
3. Construa a tabela verdade para o circuito do exercício anterior.

Álgebra de Boole

Álgebra de Boole na Wikipédia

Teoremas Booleanos

1. A . 0 = 0
2. A . 1 = A
3. A . A = A
4. A . /A = 0
5. A + 0 = A
6. A + 1 = 1
7. A + A = A
8. A + /A = 1

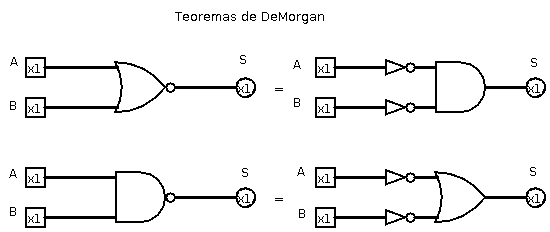
Teoremas de DeMorgan

• /(A + B) = /A . /B
• /(A . B) = /A + /B

Exercícios

• Comprovar os dois Teoremas de DeMorgam com tabelas verdade.

Laboratório e Exercícios de Simulação

Para este laboratório será utilizado o Simulador de Circuitos Lógicos - Logisim

Veja no link as instruções para download e instalação do programa.

Circuitos com portas lógicas

1. Construir e simular o circuito representado pelas expressões lógicas:
   • S = (A + B).(/B + C)
   • S = A.C + /(B.C) + /A.B.C
2. Construir e simular circuitos para comprovar experimentalmente os Teoremas de DeMorgan:
   • /(A + B) = /A . /B
   • /(A . B) = /A + /B
3. Construir e simular o circuito Ou-Exclusivo com portas AND, OR e NOT, conforme a figura:
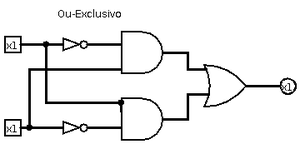
   • Represente o circuito acima como uma expressão lógica.

Referências

---

--Evandro.cantu (discussão) 10h50min de 12 de junho de 2014 (BRT)

---