Árvores: mudanças entre as edições
De Wiki Cursos IFPR Foz
Ir para navegaçãoIr para pesquisar
| Linha 5: | Linha 5: | ||
A figura ilustra uma '''árvore binária''' <ref name="TENENBAUM"/>: | A figura ilustra uma '''árvore binária''' <ref name="TENENBAUM"/>: | ||
[[Arquivo:ArvoreBinaria.png]] | [[Arquivo:ArvoreBinaria.png | 400px]] | ||
Na figura: | Na figura: | ||
| Linha 25: | Linha 25: | ||
;Árvore estritamente binária: Uma árvore é estritamente binária se todo nó que não for folha tenha as sub-árvores direita e esquerda não vazias. | ;Árvore estritamente binária: Uma árvore é estritamente binária se todo nó que não for folha tenha as sub-árvores direita e esquerda não vazias. | ||
[[Arquivo:ArvoreEstritamenteBinaria.png]] | [[Arquivo:ArvoreEstritamenteBinaria.png | 150px]] | ||
;Árvore binária completa: Uma árvore é binária completa se for uma árvore estritamente binária e todas as folhas estiverem na mesma profundidade. | ;Árvore binária completa: Uma árvore é binária completa se for uma árvore estritamente binária e todas as folhas estiverem na mesma profundidade. | ||
[[Arquivo:ArvoreBinariaCompleta.png]] | [[Arquivo:ArvoreBinariaCompleta.png | 200px]] | ||
;Outras referências: <ref>FEOFILOFF, P. | ;Outras referências: <ref>FEOFILOFF, P. | ||
Edição das 12h38min de 11 de novembro de 2014
Árvores
Uma árvore binária é uma estrutura de dados formada por um conjunto finito de elementos ou nós. Uma árvore pode esta vazia ou formada por um nó chamado raiz e dois sub-conjuntos de elementos chamados sub-árvore esquerda e sub-árvore direita. As sub-árvore esquerda e sub-árvore direita são também árvores binárias e podem estar vazias [1].
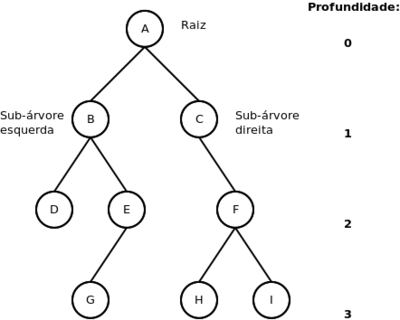
A figura ilustra uma árvore binária [1]:
Na figura:
- O nó raiz A tem duas sub-árvores B e C;
- O nó B tem duas sub-árvores D e E;
- O nó C tem apenas a sub-árvore da direita F;
- O nó E tem apenas a sub-árvore da esquerda G;
- O nó F tem duas sub-árvores H e I;
- Os nós D, G, H e I não tem sub-árvores, portanto, são chamados folhas.
Se A tem duas sub-árvores B e C, diz-se que:
- A é pai de B e C;
- B é filho esquerdo de A;
- C é filho direito de A.
- B é irmão de C.
- Profundidade da árvore binária
- Numa árvore binária, o nó raiz é considerado como profundidade 0. As sub-árvores do nó raiz profundidade 1, e assim sucessivamente. No exemplo da figura, a árvore binária tem profundidade 3.
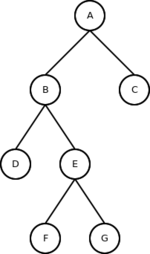
- Árvore estritamente binária
- Uma árvore é estritamente binária se todo nó que não for folha tenha as sub-árvores direita e esquerda não vazias.
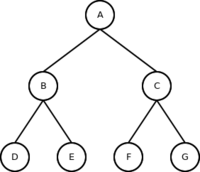
- Árvore binária completa
- Uma árvore é binária completa se for uma árvore estritamente binária e todas as folhas estiverem na mesma profundidade.
- Outras referências
- [2]
Referências
--Evandro.cantu (discussão) 09h43min de 11 de novembro de 2014 (BRST)