Laboratorio M1K Analog Devices: Filtros Eletricos: mudanças entre as edições

De Wiki Cursos IFPR Foz
Ir para navegaçãoIr para pesquisar
Linha 23: Linha 23:
#Ajuste a frequência da  '''onda senoidal''' no '''canal A''' até que a amplitude da onda no '''canal B''' seja 3,5 V.
#Ajuste a frequência da  '''onda senoidal''' no '''canal A''' até que a amplitude da onda no '''canal B''' seja 3,5 V.


==Fundamentos sobre o Capacitor==
==Fundamentos sobre Filtros RC==
 
'''Capacitores''' são dispositivos que '''armazenam energia elétrica''' em um '''campo elétrico'''. Permitem maior fluxo de corrente a medida que a frequência do sinal elétrico aumenta. Para um '''sinal senoidal''', a '''fase da corrente''' é '''adiantada''' de '''90 graus''' em relação a '''tensão'''. A unidade de '''capacitância''' é o '''Faraday (F)'''.
 
Um '''capacitor''' é formado por duas '''placas condutoras''' separadas por um  material isolante, chamado '''dielétrico'''. A '''carga''' de um '''capacitor''' é criada pela acumulação ou depleção de elétrons livres em cada placa condutora, produzindo um '''campo elétrico''' no '''dielétrico''', e, por consequência, produzindo um '''tensão elétrica''' entre as placas.
 
Uma '''carga elétrica''' (Q) sobre um '''capacitor''', produz uma '''tensão''' (V) entre as placas, em função da '''capacitância''' (C), segundo a relação:
 
<math>V (Voltz) = \frac{Q (Coulomb)}{C (Faraday)}</math>
 
ou, isolando a carga elétrica:
 
<math>Q = C V</math>
 
A '''corrente elétrica''' é definida como a quantidade de '''carga elétrica''' por unidade de '''tempo'''. É expressa matematicamente como a '''derivada da carga elétrica no tempo''':
 
<math>I(t) =  \frac{dQ(t)}{dt} = C \frac{dV(t)}{dt}</math>
 
ou seja, a '''corrente''' no capacitor é função da '''derivada da tensão no tempo''', multiplicada pela capacitância.
 
A derivada indica que a corrente elétrica no capacitor é maior quanto maior for a variação da tensão. Desta forma, para uma '''tensão senoidal''', quanto maior a '''frequência''', maior o fluxo da '''corrente'''. Para uma '''tensão constante''', a '''corrente''' no capacitor é '''zero'''.


==Fundamentos sobre o Circuito RC==
==Fundamentos sobre o Circuito RC==

Edição das 13h25min de 13 de julho de 2020

Laboratório: Introdução aos filtros elétricos

Este laboratório foi baseado no material disponibilizado pela Analog Devices, fabricante do módulo educacional M1K Analog Devices: [1]

Objetivos

Conhecer o princípio de funcionamento dos filtros elétricos RC passa baixa e passa alta.

Equipamento e Materiais

  • Modulo Analog Devices M1K e software Pixelpulse
  • Componentes Eletrônicos:
    • Resistores: 68Ω,100Ω 10KΩ, 200KΩ
    • Capacitores: 10uF, 22uF e 47uF
    • Leds
    • Diodo 1N914
    • Circuito Integrado AD8561

Procedimentos Práticos

  1. Identifique os resistores e capacitores a serem utilizados no experimento. Observe que os capacitores eletrolíticos tem polaridade, portanto, devem ser montados no circuito considerando os terminais positivo e negativo.
  2. Monte na matriz de contatos o filtro RC da figura, usando o resistor de 68Ω e o capacitor de 22uF: 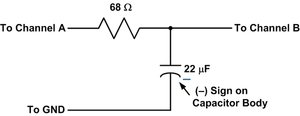[1]
  3. Selecione o canal A do módulo Analog Devices M1K para Gerar Tensão/Medir Corrente e o canal B para Medir Voltagem.
  4. Configure o canal A para gerar uma onda senoidal com 10 Hz de frequência e tensão variando de 0 V a 5 V. Observe no canal B a forma de onda sobre o capacitor.
  5. Gradualmente aumente a frequência da onda senoidal até 1000 Hz e observe no canal B a redução da amplitude da forma de onda sobre o capacitor.
  6. Ajuste a frequência da onda senoidal no canal A até que a amplitude da onda no canal B seja 3,5 V.

Fundamentos sobre Filtros RC

Fundamentos sobre o Circuito RC

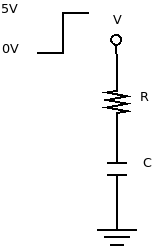
Num circuito RC série, quando um degrau de tensão é aplicado, inicialmente toda tensão aparece toda sobre o resistor, pois o capacitor está descarregado e a tensão sobre ele é zero. A corrente inicial que fluirá no circuito será dada pela Lei de Ohm (I = V / R) e vai ser responsável por iniciar a carga do capacitor. A medida que o capacitor vai sendo carregado, a tensão sobre ele vai aumentando, diminuindo a tensão resultante sobre o resistor, segundo a Lei de Kirchoff, e, consequentemente, diminuindo também a corrente no circuito. Quanto o capacitor se carregar totalmente, a tensão de 5V estará toda sobre o capacitor e a corrente no circuito será reduzida a zero.

O processo de carga do capacitor segue uma curva que desacelera exponencialmente a medida que a tensão sobre o capacitor aumenta. A taxa de crescimento da carga do capacitor depende do produto RC, chamado de constante de tempo (segundos) e é representado pela letra grega tau (τ). Numa constante de tempo o capacitor é carregado com 63% de sua carga. Em cinco constantes de tempo a carga do capacitor chega a 99.3%. O tempo da carga total tende ao infinito, entretanto, na prática, considera-se que em cinco constantes de tempo o capacitor está carregado.

Num circuito RC série, a tensão sobre o capacitor (VC), em função da tensão total aplicada (VT) é dada pela expressão:

No primeiro circuito, a constante de tempo era de (100 KΩ)*(47 μF) = 4.7 segundos, fazendo com que a carga/descarga total do capacitor fosse de cerca de 23,5 segundos.

Observações e Conclusões

  • '

Referências

  1. ↑ 1,0 1,1 https://wiki.analog.com/university/courses/engineering_discovery/lab_5

Evandro.cantu (discussão) 10h03min de 13 de julho de 2020 (-03)

Disponível em “http://wiki.foz.ifpr.edu.br/wiki/index.php?title=Laboratorio_M1K_Analog_Devices:_Filtros_Eletricos&oldid=26755”