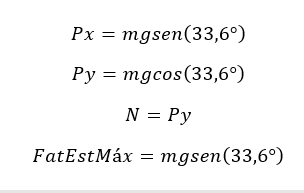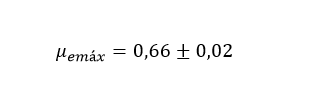Portfólio: Zatch Bell: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 54: | Linha 54: | ||
[[Arquivo: Plano_Inclinado_Evandro_Pedro.png]] | [[Arquivo: Plano_Inclinado_Evandro_Pedro.png]] | ||
==Experimento: Determinação do Coeficiente de Atrito Estático no Plano inclinado== | |||
Os Participantes deste experimento foram: | |||
Cristopher | |||
Evandro Andretti | |||
Fernando Reis | |||
Patricia Reis | |||
Pedro Reis | |||
===Introdução=== | |||
'''Força de Atrito''' | |||
A força de atrito é uma força que se opõe ao movimento dos corpos. Ela pode ser estática, se o corpo estiver em repouso, ou dinâmica, para corpos em movimento. <ref>HALLIDAY, David; RESNIK, Robert; WALKER, Jearl. '''Fundamentos da Física''', 10 ed. LTC, 2016. </ref> <ref>MAXIMO, A.; ALVARENGA, B., '''Física: volume único'''. Scipione, 1997 </ref> | |||
Considere um corpo que é puxado, porém não consegue escorregar na superfície, significa que ele recebeu a ação de uma força de atrito que impede seu movimento. Essa força é denominada atrito estático. Nesse caso: | |||
F = FAE | |||
A força de atrito estático tem um limite máximo, denominado tem um limite máximo, denominado de força de atrito estático máximo. | |||
FAEmax = μe . N | |||
N é a força normal que o corpo troca com a superfície do apoio; | |||
μe é o coeficiente de atrito estático. | |||
O coeficiente é um numero adimensional que depende das rugosidades da face do corpo que está apoiada e da superfície de contato. Quanto mais áspero for o corpo ou a superfície maior será o coeficiente. | |||
A força de atrito estático pode variar de zero ate seu limite máximo, em função da intensidade da força aplicada. Então o corpo so deslizará na superfície quando a força F vencer o atrito estático. | |||
'''Atrito Dinâmico''' | |||
Também chamado de atrito cinético, o atrito dinâmico ocorre quando a força do atrito estático for superada, de modo que os dois corpos entram em movimento, gerando, assim, uma menor força de atrito, por exemplo, empurrar a pedra depois que ela entrou em movimento. | |||
Para calcular a força do atrito dinâmico, utiliza-se a expressão: Fatd = μd.N, donde μd corresponde ao coeficiente do atrito dinâmico e N, a força normal. | |||
===Objetivo=== | |||
Determinar um valor experimental para o coeficiente de atrito estático máximo sem o auxílio de um dinamômetro (desconhecendo o peso do objeto) utilizando como instrumentos de medida apenas régua e transferidor. | |||
===Materiais e Métodos=== | |||
Os materiais utilizados neste experimento: | |||
1. Plano inclinado | |||
2. Régua | |||
3. Transferidor | |||
4. Corpo de prova | |||
5. Calculadora | |||
6. Caneta e papel | |||
Para realizar a atividade inicialmente foi determinado qual a posição próxima da iminência de movimento do corpo no plano inclinado. Com esta posição determinada foi calculado inicialmente de duas formas diferentes para obter o ângulo de abertura, a primeira maneira foi com o auxílio da régua e determinou-se os valores do triângulo formado (ver imagens abaixo) e com isso o ângulo formado. A segunda forma foi medindo diretamente o ângulo com o auxílio do transferidor considerando o triângulo interno (ver figuras abaixo) que é semelhante ao triângulo externo. Com o método que melhor representa o ângulo encontrado repetiu-se o experimento um total de 10 vezes. | |||
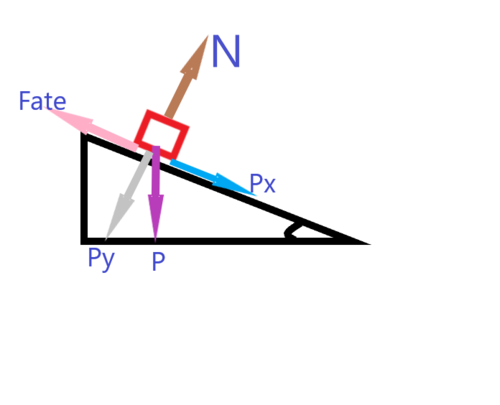
Considerando então o problema, desenhou-se um esboço para indicar as forças de atuação para em seguida construir o diagrama de corpo livre: | |||
o ângulo entre Py e P é o mesmo ângulo do triângulo que determinou-se nas medidas e que consideraremos para apresentação o valor da média 33,6°. | |||
[[Arquivo:diagrama1patinandoatritoestatico.png|500px]] | |||
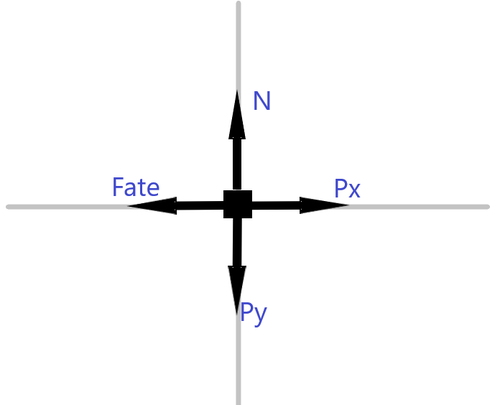
Com o desenho em mãos obteve-se o diagrama de corpo livre abaixo: | |||
[[Arquivo:diagramacorpolivrepatinandoatritoestatico.png|500px]] | |||
de posse do diagrama de corpo livre e do valor do ângulo, determinar o coeficiente de atrito estático tornou-se consequência natural, decompôs-se o peso P em Px e Py onde o primeiro foi dado por Px=P.sen(33,6°) e Py=P.cos(33,6°). Considerando o sistema em equilíbrio equacionou-se as forças no eixo x e no eixo y onde obteve-se que o coeficiente de atrito estático coincide com a tangente do ângulo calculado. | |||
[[Arquivo:dadoscoefpatinandoestatico.png|500px]] | |||
====Imagens==== | |||
[[Arquivo:imagemexperimentocoeficientedeatritoestaticopatinando(1).jpeg|500px]] | |||
[[Arquivo:imagemexperimentocoeficientedeatritoestaticopatinando(2).jpeg|500px]] | |||
[[Arquivo:imagemexperimentocoeficientedeatritoestaticopatinando(4).jpeg|500px]] | |||
===Reultados=== | |||
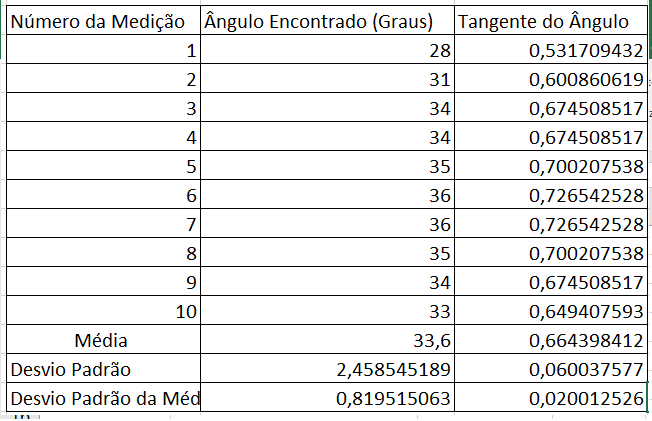
Como viu-se que o coeficiente de atrito estático máximo acaba sendo definido pela tangente do ângulo abaixo apresenta-se uma tabela com o valor das medições e o tratamento estatístico de desvio padrão e desvio padrão da média tanto para o ângulo quanto para a tangente. | |||
[[Arquivo:planilhacoeficientepatinando.png]] | |||
assim, neste experimento obteve-se o valor de | |||
[[Arquivo:coefatriestmaxpatinandohenry.png]] | |||
===Conclusão=== | |||
Edição das 18h21min de 9 de outubro de 2018
Zatch Bell
- Curso
- Licenciatura em Física
- Disciplina
- Informática Aplicada ao Ensino de Física
- Professor
- Evandro Cantú
- Equipe
- Evandro Carlos Andretti
- Pedro Luís dos Reis
Tópico 1: Tempo de reação humana
Experimento: Tempo de reação humana
O experimento teve com objetivo medir o tempo de reação humana, utilizando uma régua de 30 cm, a qual foi deixada cair e capturada antes de cair no chão. O tempo de reação foi medido com um cronometro com dois cliques.
Tópico 2
Experimento: Gráfico com Planilha de Calculo
Nesse experimento consideramos a velocidade de uma queda livre.
Tópico 3: Plano Inclinado
Introdução ao Tema
Neste experimento realizamos o tempo de caída de uma bolinha, calculando a velocidade média e a velocidade instantânea, e nisso, usamos para ver a queda, fizemos muitas realizações das medidas. Analisamos o movimento de uma bolinha em uma queda com pouca elevação.
Objetivo
O objetivo principal era calcularmos a velocidade média da queda.
Material e Procedimento
Material: Utilizamos uma trena, uma lampada de led de aproximadamente 1 metro e 20 centímetros, uma esfera, e um cronômetro Procedimento: Com intervalos de 10 em 10 centímetros na lampada, colocamos a bolinha na posição inicial, fazendo-a com que ela desça sem ajuda externa, e filmando de cima, com dois cronômetros ao lado, e depois, passamos o video para o computador, vendo em câmera lenta, e vendo com perfeição o horário certo com que foi passado por todos os pontos.
Fórmula simples:
y = ax + b
Fórmula complexa:
s = s0 + v0 t + 1/2 a t2
Desenho
Experimento: Determinação do Coeficiente de Atrito Estático no Plano inclinado
Os Participantes deste experimento foram: Cristopher Evandro Andretti Fernando Reis Patricia Reis Pedro Reis
Introdução
Força de Atrito
A força de atrito é uma força que se opõe ao movimento dos corpos. Ela pode ser estática, se o corpo estiver em repouso, ou dinâmica, para corpos em movimento. [1] [2]
Considere um corpo que é puxado, porém não consegue escorregar na superfície, significa que ele recebeu a ação de uma força de atrito que impede seu movimento. Essa força é denominada atrito estático. Nesse caso:
F = FAE
A força de atrito estático tem um limite máximo, denominado tem um limite máximo, denominado de força de atrito estático máximo.
FAEmax = μe . N
N é a força normal que o corpo troca com a superfície do apoio; μe é o coeficiente de atrito estático.
O coeficiente é um numero adimensional que depende das rugosidades da face do corpo que está apoiada e da superfície de contato. Quanto mais áspero for o corpo ou a superfície maior será o coeficiente. A força de atrito estático pode variar de zero ate seu limite máximo, em função da intensidade da força aplicada. Então o corpo so deslizará na superfície quando a força F vencer o atrito estático.
Atrito Dinâmico
Também chamado de atrito cinético, o atrito dinâmico ocorre quando a força do atrito estático for superada, de modo que os dois corpos entram em movimento, gerando, assim, uma menor força de atrito, por exemplo, empurrar a pedra depois que ela entrou em movimento.
Para calcular a força do atrito dinâmico, utiliza-se a expressão: Fatd = μd.N, donde μd corresponde ao coeficiente do atrito dinâmico e N, a força normal.
Objetivo
Determinar um valor experimental para o coeficiente de atrito estático máximo sem o auxílio de um dinamômetro (desconhecendo o peso do objeto) utilizando como instrumentos de medida apenas régua e transferidor.
Materiais e Métodos
Os materiais utilizados neste experimento: 1. Plano inclinado 2. Régua 3. Transferidor 4. Corpo de prova 5. Calculadora 6. Caneta e papel
Para realizar a atividade inicialmente foi determinado qual a posição próxima da iminência de movimento do corpo no plano inclinado. Com esta posição determinada foi calculado inicialmente de duas formas diferentes para obter o ângulo de abertura, a primeira maneira foi com o auxílio da régua e determinou-se os valores do triângulo formado (ver imagens abaixo) e com isso o ângulo formado. A segunda forma foi medindo diretamente o ângulo com o auxílio do transferidor considerando o triângulo interno (ver figuras abaixo) que é semelhante ao triângulo externo. Com o método que melhor representa o ângulo encontrado repetiu-se o experimento um total de 10 vezes.
Considerando então o problema, desenhou-se um esboço para indicar as forças de atuação para em seguida construir o diagrama de corpo livre: o ângulo entre Py e P é o mesmo ângulo do triângulo que determinou-se nas medidas e que consideraremos para apresentação o valor da média 33,6°.
Com o desenho em mãos obteve-se o diagrama de corpo livre abaixo:
de posse do diagrama de corpo livre e do valor do ângulo, determinar o coeficiente de atrito estático tornou-se consequência natural, decompôs-se o peso P em Px e Py onde o primeiro foi dado por Px=P.sen(33,6°) e Py=P.cos(33,6°). Considerando o sistema em equilíbrio equacionou-se as forças no eixo x e no eixo y onde obteve-se que o coeficiente de atrito estático coincide com a tangente do ângulo calculado.
Imagens
Reultados
Como viu-se que o coeficiente de atrito estático máximo acaba sendo definido pela tangente do ângulo abaixo apresenta-se uma tabela com o valor das medições e o tratamento estatístico de desvio padrão e desvio padrão da média tanto para o ângulo quanto para a tangente.
assim, neste experimento obteve-se o valor de