Sistemas de Controle: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 94: | Linha 94: | ||
<math>{U_s \over E_s} = K_p (1 + {1 \over T_i s} + T_d s) </math> | <math>{U_s \over E_s} = K_p (1 + {1 \over T_i s} + T_d s) </math> | ||
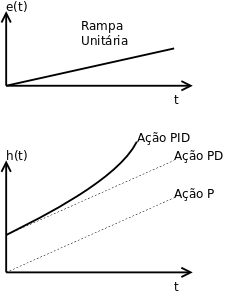
'''Gráfico do Controle Proporcional Integral Derivativo''': | |||
[[Arquivo:GraficoPID.png]] | |||
==Referências== | ==Referências== | ||
Edição das 21h19min de 5 de maio de 2018
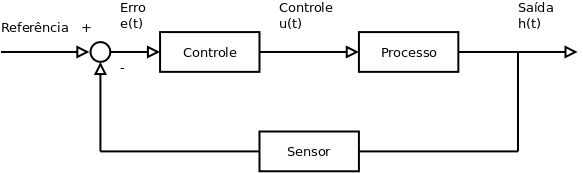
Sistemas de Controle
Referências: [1].
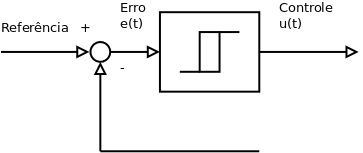
Controle On / Off
É interessanete a ação de controle on/off ter um intervalo diferencial, para evitar comutações excessivas.
Falhou ao verificar gramática (função desconhecida '\begin{matrix}'): {\displaystyle u(t) = \left \{ \begin{matrix} U_1, & \mbox{se e(t) > 0} \\ U_2, & \mbox{se e(t) < 0} \end{matrix} \right. }
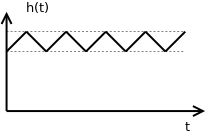
Gráfico da saída com controle On/Off:
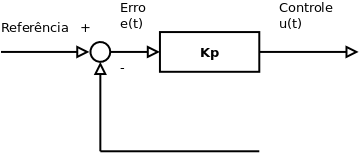
Controle Proporcional
Função de Transferência (Transformada de Laplace):
A ação de controle proporcional funciona como um amplificador com ganho variável, proporcional ao erro.
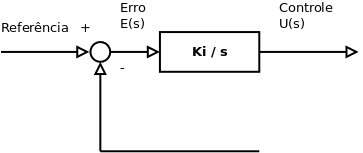
Controle Integral
Função de Transferência (Transformada de Laplace):
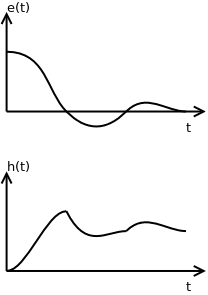
Na ação de controle integral a saída do controlador é igual a área sobre a curva do erro (integral do erro) atuante até aquele instante de tempo.
Quando o erro fica nulo a ação de controle permanece num estado estacionário.
Gráfico do Controle Integral:
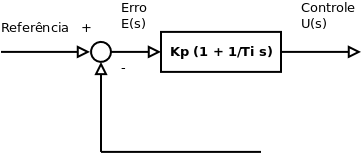
Controle Proporcional Integral
onde, Ti é o tempo integral.
Função de Transferência (Transformada de Laplace):
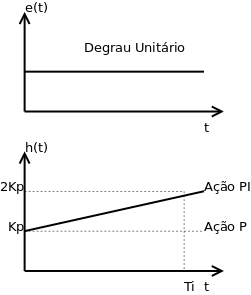
Sem o controle integral há um erro estacionário (também chamado erro residual) inerente ao controle proporcional.
Gráfico do Controle Proporcional Integral:
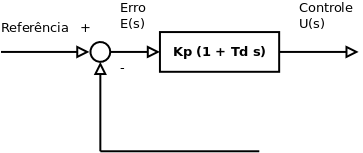
Controle Proporcional Derivativo
onde, Td é o tempo derivativo.
Função de Transferência (Transformada de Laplace):
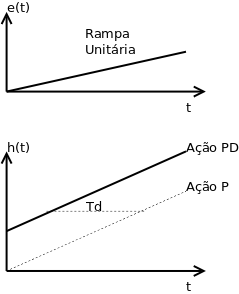
A ação do controle derivativo é proporcional a taxa de variação do erro atuante. Deve ser usada em períodos transitórios.
Gráfico do Controle Proporcional Derivativo:
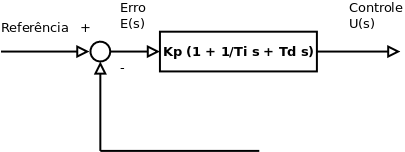
Controle Proporcional Integral Derivativo
onde, Ti é o tempo integral e Td é o tempo derivativo.
Função de Transferência (Transformada de Laplace):
Gráfico do Controle Proporcional Integral Derivativo:
Referências
- ↑ OGATA, Katsuhiko. Engenharia de Controle Moderno, LTC, 2011.
--Evandro.cantu (discussão) 19h03min de 4 de maio de 2018 (BRT)