Frequência e período de um sinal periódico: mudanças entre as edições
| Linha 4: | Linha 4: | ||
A unidade de medida de '''frequência''' é o '''Hertz (Hz)''': | A unidade de medida de '''frequência''' é o '''Hertz (Hz)''': | ||
1 Hz = 1 ciclo/segundo | |||
1 | 10 Hz = 10 ciclo/segundo | ||
1 | 100 Hz = 100 ciclo/segundo | ||
1 | 1 K Hz = 1000 (ou 10<sup>3</sup>) ciclos/segundo | ||
1 M Hz = 10<sup>6</sup> ciclos/segundo | |||
1 G Hz = 10<sup>9</sup> ciclos/segundo | |||
;Relação entre frequência (f) e período (T): | ;Relação entre frequência (f) e período (T): | ||
Edição das 21h19min de 30 de maio de 2017
Frequência e período de um sinal periódico
A frequência é uma grandeza física que indica o número de ocorrências de um evento (ciclo ou oscilações) em um determinado intervalo de tempo. Esse tempo recebe o nome de período (T).
A unidade de medida de frequência é o Hertz (Hz):
1 Hz = 1 ciclo/segundo 10 Hz = 10 ciclo/segundo 100 Hz = 100 ciclo/segundo 1 K Hz = 1000 (ou 103) ciclos/segundo 1 M Hz = 106 ciclos/segundo 1 G Hz = 109 ciclos/segundo
- Relação entre frequência (f) e período (T)
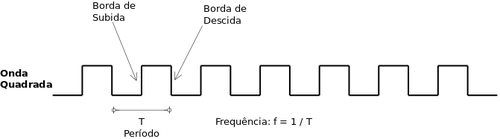
f = 1 / T
Sinais Digitais
Os sinais digitais periódicos geralmente são ondas quadradas, com os níveis lógicos LOW (0 V) e HIGH (5 V). A transição LOW para HIGH é chamada transição positiva (borda de subida) e a transição de HIGH para LOW é chamada transição negativa (borda de descida).
Sinais Analógicos
Os sinais analógicos apresentam variação de amplitude contínua no tempo. Uma das formas de onda analógicas mais simples é a sonda senoidal, a qual obedece a uma função seno.
Por exemplo, a tensão alternada fornecida pelas empresas de distribuição de energia elétrica padronizada no Brasil é uma onda senoidal com frequência de:
60 Hz = 60 ciclos/segundo
Todas as outras formas de onda, mesmo as mais complexas, podem ser decompostas em conjuntos de ondas senoidais através da aplicação das séries de fourier [1].
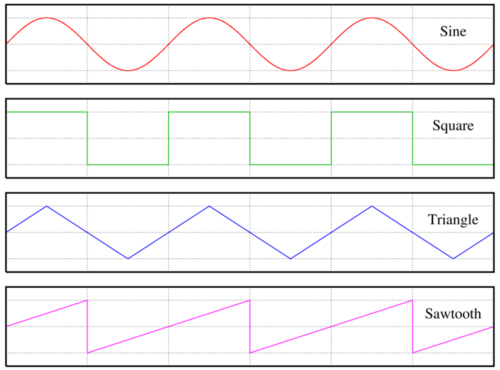
A figura abaixo ilustra diversas formas de onda de sinais periódicos, incluindo ondas senoidal, quadrada, triangular e dente de serra.
Referências
--Evandro.cantu (discussão) 09h27min de 19 de abril de 2017 (BRT)