Árvores: mudanças entre as edições
| (74 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
=Árvores= | =Árvores= | ||
Uma '''árvore binária''' é uma '''estrutura de dados''' formada por um conjunto finito de elementos ou '''nós'''. Uma árvore pode | Uma '''árvore binária''' é uma '''estrutura de dados''' formada por um conjunto finito de elementos ou '''nós'''. Uma árvore pode estar vazia ou pode ser formada por um nó chamado '''raiz''' e dois sub-conjuntos de elementos chamados '''sub-árvore esquerda''' e '''sub-árvore direita'''. As sub-árvores esquerda e direita são também árvores binárias e podem estar vazias <ref name="TENENBAUM">[[Mídia:EstruturaDadosC.pdf | TENENBAUM, Aaron M.; LANGSAM, Yedidyah; AUGENSTEIN, Moshe. Estruturas de dados usando C. Árvores, p. 323, Makron Books, 1995.]]</ref>. | ||
A figura ilustra uma '''árvore binária''' <ref name="TENENBAUM"/>: | A figura abaixo ilustra uma '''árvore binária''' <ref name="TENENBAUM"/>: | ||
[[Arquivo:ArvoreBinaria.png | 400px]] | [[Arquivo:ArvoreBinaria.png | 400px]] | ||
Na figura: | Na figura: | ||
*O nó raiz A tem duas sub-árvores B e C; | *O nó '''raiz''' A tem duas '''sub-árvores''' B e C; | ||
*O nó B tem duas sub-árvores D e E; | *O nó B tem duas sub-árvores D e E; | ||
*O nó C tem apenas a sub-árvore da direita F; | *O nó C tem apenas a sub-árvore da direita F; | ||
| Linha 31: | Linha 31: | ||
[[Arquivo:ArvoreBinariaCompleta.png | 200px]] | [[Arquivo:ArvoreBinariaCompleta.png | 200px]] | ||
== | ==Exemplo de aplicação das árvores binárias== | ||
As '''árvores binárias''' são uma estrutura de dados útil quando precisam ser tomadas '''decisões bi-direcionais''' em cada ponto do processo. Por exemplo, suponha que queiramos encontrar repetições em uma lista de números. Uma maneira de fazer isto é comparar cada número com todos os que o precedem. Entretanto, isto pode envolver muitas comparações. Outra maneira é utilizar uma árvore binária | As '''árvores binárias''' são uma estrutura de dados útil quando precisam ser tomadas '''decisões bi-direcionais''' em cada ponto do processo. Por exemplo, suponha que queiramos '''encontrar repetições em uma lista de números'''. Uma maneira de fazer isto é comparar cada número com todos os que o precedem. Entretanto, isto pode envolver muitas comparações. Outra maneira é utilizar uma árvore binária <ref name="TENENBAUM"/>. | ||
Suponha que temos a seguinte lista de números para verificar repetições: | Suponha que temos a seguinte lista de números para verificar repetições: | ||
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 | 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 | ||
Neste caso, iniciamos a ''' | Neste caso, iniciamos a árvore com o '''primeiro número''' da lista como sendo o nó '''raiz'''. Na sequência, comparamos o próximo número com o número da raiz, se for '''igual''' é uma '''repetição'''. Se for '''menor''', comparamos com a '''sub-árvore da esquerda'''. Se for '''maior''', comparamos com a '''sub-árvore da direita'''. Se a sub-árvore estiver '''vazia''', incluímos o número como '''filho''' desta sub-árvore, a esquerda ou direita, caso seja menor ou maior que o conteúdo do nó, respectivamente. | ||
Veja a árvore que seria construída neste exemplo: | Veja a árvore que seria construída neste exemplo: | ||
| Linha 48: | Linha 47: | ||
Diferentemente de uma '''lista''', na qual os nós são percorridos de maneira '''linear''', numa '''árvore''', existem '''diferentes ordens''' para poder percorrê-la. | Diferentemente de uma '''lista''', na qual os nós são percorridos de maneira '''linear''', numa '''árvore''', existem '''diferentes ordens''' para poder percorrê-la. | ||
Todos os métodos para percorrer uma árvore são definidos '''recursivamente''', de modo que percorrer uma árvore envolve visitar a '''raiz''' e depois a '''sub-árvore direita''' e a '''esquerda'''. O que difere cada método é a ordem em que estas operações são realizadas <ref name="TENENBAUM"/>. | |||
Três métodos são conhecidos para percorrer uma árvore binária: | |||
*'''Em ordem''', ou '''esquerda-raiz-direita'''; | |||
*'''Pré-ordem''' ou '''percurso em profundidade''' ou '''raiz-esquerda-direita'''; | |||
*'''Pós-ordem''' ou '''esquerda-direita-raiz'''. | |||
Por exemplo, dada a árvore: | |||
A | |||
/ \ | / \ | ||
B C | |||
/ / \ | / / \ | ||
D E F | |||
/ \ \ | / \ \ | ||
0 2 7 | G H I | ||
;Percorrer a árvore em ordem: Percorre-se primeiro a '''sub-árvore esquerda''', na ordem '''esquerda-raiz-direita'''. Depois a '''raiz'''. E depois a '''sub-árvore direita''', também na ordem esquerda-raiz-direita <ref name="FEOFILOFF"> FEOFILOFF, P. IME-USP, 2013. http://www.ime.usp.br/~pf/algoritmos/aulas/bint.html.</ref>: | |||
4 | |||
/ \ | |||
3 7 | |||
/ / \ | |||
1 5 8 | |||
/ \ \ | |||
0 2 6 | |||
;Percorrer a árvore em pré-ordem ou em profundidade: Percorre-se primeiro a '''raiz'''. Depois a '''sub-árvore esquerda''', na ordem '''raiz-esquerda-direita'''. E depois a '''sub-árvore direita''', também na ordem raiz-esquerda-direita: | |||
0 | |||
/ \ | |||
1 5 | |||
/ / \ | |||
2 6 8 | |||
/ \ \ | |||
3 4 7 | |||
;Percorrer a árvore em pós-ordem: Percorre-se primeiro a '''sub-árvore esquerda''', na ordem '''esquerda-direita-raiz'''. Depois a '''sub-árvore direita''', também na ordem esquerda-direita-raiz. E depois a '''raiz''': | |||
8 | |||
/ \ | |||
3 7 | |||
/ / \ | |||
2 5 6 | |||
/ \ \ | |||
0 1 4 | |||
==Inserção de elementos em árvores binárias== | |||
Vários algoritmos que trabalham com árvores trabalham em duas fases. Primeiro '''inserem elementos na árvore''' e depois '''percorrem a árvore'''. | |||
Veja um exemplo de '''classificação de números em ordem ascendente'''. A medida que os números forem sendo lidos os mesmos vão sendo inseridos na árvore. Entretanto, ao contrário do algoritmo usado para achar repetições, aqui os números repetidos também são inseridos na árvore. Quando um novo número é comparado com a raiz da árvore, a '''sub-árvore esquerda''' é utilizada para inserir se o número for '''menor''' que o conteúdo do nó e a '''sub-árvore direita''' é usada se o número for '''maior ou igual''' ao conteúdo do nó<ref name="TENENBAUM"/>. | |||
Para a lista de números | |||
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 | |||
a árvore resultante seria: | |||
[[Arquivo:ArvoreInsercao.png | 300px]] | |||
Note que nesta árvore, todos os elementos da esquerda do nó raiz são menores que os elementos da direita, valendo o mesmo para cada sub-árvore. | |||
;Exercício: | |||
'''Percorra a árvore''' gerada anteriormente '''em ordem''', ou '''esquerda-raiz-direita''' e veja a ordem dos números. | |||
==Implementação de árvores em linguagem C== | ==Implementação de árvores em linguagem C== | ||
Cada nó de uma '''árvore''' pode ser implementado em linguagem C como uma '''estrutura''' com três campos: um campo '''conteúdo''', para guardar a informação deste nó, e dois campos tipo '''ponteiro''' que apontam para as '''sub-árvores direita''' e '''esquerda'''. | Cada nó de uma '''árvore''' pode ser implementado em linguagem C como uma '''estrutura''' com três campos: um campo '''conteúdo''', para guardar a informação deste nó, e dois campos tipo '''ponteiro''' que apontam para as '''sub-árvores direita''' e '''esquerda'''. | ||
Os códigos abaixo foram adaptados da referência <ref name="WIKILIVROS">WIKILIVROS: Programar em C / Árvores Binárias http://pt.wikibooks.org/wiki/Programar_em_C/%C3%81rvores_bin%C3%A1rias</ref>. | |||
===Declaração de um nó de uma árvore=== | ===Declaração de um nó de uma árvore=== | ||
| Linha 75: | Linha 120: | ||
</source> | </source> | ||
Note que a declaração do nó da árvore é recursiva, onde os ponteiros *esq e *dir apontam para estruturas do mesmo tipo que está sendo declarada. | Note que a '''declaração''' do nó da árvore é '''recursiva''', onde os ponteiros *esq e *dir apontam para estruturas do mesmo tipo que está sendo declarada. | ||
===Criação de uma árvore e sua definição recursiva=== | |||
Uma árvore é criada a partir da declaração do endereço de sua raiz, fazendo seu ponteiro apontar para NULL, que caracteriza uma árvore vazia. | |||
<source lang="c"> | |||
#include <stdio.h> | |||
#include <stdlib.h> | |||
main() | |||
{ | |||
arvore *r = NULL; //r é um ponteiro para uma árvore vazia | |||
... | |||
} | |||
</source> | |||
Como uma '''árvore binária''' pode estar vazia ou possuir sub-árvores direita e/ou esquerda. Portanto, uma '''árvore binária''' pode ser definida de maneira '''recursiva''', como segue: | |||
:Um objeto '''r''' é uma '''árvore binária''' se: | |||
:*'''r''' é '''NULL''' ou | |||
:*'''r->esq''' e '''r->dir''' são '''árvores binárias'''. | |||
===Funções recursivas para percorrer uma árvore binária=== | |||
;Em ordem: Faz a varredura '''esquerda-raiz-direita (e-r-d): | |||
<source lang="c"> | |||
void imprime_erd(arvore *r) { | |||
if (r != NULL) { | |||
imprime_erd(r->esq); | |||
printf("%d\n", r->conteudo); | |||
imprime_erd(r->dir); | |||
} | |||
} | |||
</source> | |||
;Pré-ordem: Faz a varredura em '''profundidade''' ou '''raiz-esquerda-direita (r-e-d): | |||
<source lang="c"> | |||
void imprime_red(arvore *r) { | |||
if (r != NULL) { | |||
printf("%d\n", r->conteudo); | |||
imprime_red(r->esq); | |||
imprime_red(r->dir); | |||
} | |||
} | |||
</source> | |||
;Pós-ordem: Faz a varredura '''esquerda-direita-raiz (e-d-r): | |||
<source lang="c"> | |||
void imprime_edr(arvore *r) { | |||
if (r != NULL) { | |||
imprime_edr(r->esq); | |||
imprime_edr(r->dir); | |||
printf("%d\n", r->conteudo); | |||
} | |||
} | |||
</source> | |||
===Função recursiva para inserção em árvores binárias=== | |||
Esta função '''recursiva''' insere na árvore binária à esquerda se o número for menor que a raiz ou à direita se maior ou igual: | |||
<source lang="c"> | |||
void inserir(arvore **r, int num){ | |||
if(*r == NULL){ | |||
*r = (arvore *) malloc(sizeof(arvore)); | |||
(*r)->esq = NULL; | |||
(*r)->dir = NULL; | |||
(*r)->conteudo = num; | |||
}else{ | |||
if(num < (*r)->conteudo) | |||
inserir(&(*r)->esq, num); | |||
else | |||
inserir(&(*r)->dir, num); | |||
} | |||
} | |||
</source> | |||
Alguns conceitos: | |||
:;Ponteiro: | |||
:*Um '''ponteiro''' aponta para um '''endereço de memória'''. | |||
:*Se '''ponteiro=NULL''' ele aponta para '''nada'''. | |||
:Quando uma '''árvore binária''' é '''criada''' o ponteiro aponta para nada: | |||
arvore *r=NULL; | |||
:Quando vou '''inserir''' um elemento em uma árvore: | |||
:*Um nó é criado: | |||
*r = (arvore *) malloc(sizeof(arvore)); | |||
::O '''conteúdo do ponteiro''' (*r) recebe '''endereço do novo nó''' criado. | |||
;Exemplo ilustrativo: A figura apresenta uma sequência de operações, na qual uma árvore binária é primeiramente criada e em seguida são inseridos os números 22, 33 e 11, nesta ordem. Os endereços de memória da figura são apenas ilustrativos. | |||
[[Arquivo:ArvoreInserir.png]] | |||
===Remoção de nós de uma árvore=== | |||
Numa '''árvore binária''' todos os elementos à esquerda do nó raiz são menores que os elementos à direita, valendo o mesmo para cada sub-árvore. Assim, se um nó for removido, esta característica da árvore binária deve ser respeitada. | |||
Algumas regras para '''remover nós''' de uma '''árvore binária''': | |||
[[Arquivo:ArvoreRemover.png | 300px]] | |||
#Se o nó é uma '''folha''', isto é, '''não tem sub-árvores''', o mesmo pode ser removido sem problemas. Em seguida deve-se fazer o ponteiro de seu pai apontar para NULL. | |||
#*Caso do nó G da figura. | |||
#:[[Arquivo:ArvoreRemoverFolha.png | 150px]] | |||
#Se o nó '''tem somente uma sub-árvore''' (direita ou esquerda), podemos eliminar o nó "puxar" o nó filho para seu lugar. | |||
#*Caso do nó D da figura. | |||
#:[[Arquivo:ArvoreRemoverSubArvore.png | 150px]] | |||
#Se o nó '''tem as duas sub-árvores''' há duas possibilidades: podemos "puxar" para seu lugar o '''maior elemento da sub-árvore esquerda''' ou o '''menor elemento da sub-árvore direita''' | |||
#*Caso do nó A da figura, podemos substitui-lo pelo maior elemento da sub-árvore esquerda, no caso o nó E, ou pelo menor elemento da sub-árvore direita, no caso o nó F. | |||
#:[[Arquivo:ArvoreRemoverDuasSubArvores.png | 350px]] | |||
Veja função para '''remover''' nós em <ref name="WIKILIVROS"/>, além de funções para verificar a profundidade de uma árvore, contar o número de nós e contar o número de folhas. | |||
===Exercícios=== | |||
#Compile e teste as funções para '''declarar''', '''criar''', '''inserir''' e '''fazer a varredura''' dos nós de uma '''árvore binária'''. | |||
#Construa um programa que utilize '''árvores binárias''' para encontrar '''repetições''' em uma lista de números, como no exemplo visto anteriormente. | |||
#Construa um programa que utilize '''árvores binárias''' para '''ordenamento ascendente''' de uma sequência de números, como no exemplo visto anteriormente. | |||
#Modifique o programa para fazer o '''ordenamento descendente''' de uma sequência de números. | |||
#Implemente função para '''remover''' elementos de uma árvore, considerando que não há elementos duplicados. | |||
#Implemente funções para: | |||
#*verificar a '''profundidade''' de uma árvore, | |||
#*contar o '''número de nós''' de uma árvore, | |||
#*contar o '''número de folhas''' de uma árvore. | |||
====Problema==== | |||
Considere um sistema de votação por telefone, no qual cada número pode votar apenas uma vez. Considere ainda que o sistema vai armazenar os números de telefones que já votaram em uma estrutura de dados tipo árvore binária visando facilitar a busca para verificar se um dado número já votou. | |||
*Suponha de num dado momento 1 milhão de votos já tenham sido realizados. Responda quantos nós tenho que visitar, no máximo, para saber se o número de uma nova ligação já votou ou não? | |||
====Trabalho==== | |||
#Apresentar código documentado com conjunto de funções para trabalhar com '''árovores binárias''', incluindo funções para '''inserir''' e '''fazer a varredura''' e '''remover''' dos nós de uma árvore binária. | |||
#Utilize as funções para árvores binárias em programas que realizem as seguintes operações: | |||
##Ordenar uma lista de 100 números inteiros; | |||
##Ler uma lista de 100 números inteiros de um arquivo e imprimir em outro arquivo a lista dos números ordenada; | |||
##Ler uma lista de 100 números inteiros de um arquivo e inserir em uma árvore binária. Em seguida, solicitar ao usuário a inserção ou remoção de números na árvore. No caso de inserção o programa deve verificar se o número já está na árvore e incluí-lo se não estiver. No caso de remoção o programa deve verificar se o número está na árvore antes de removê-lo. Ao fim, imprimir em arquivo a lista de números ordenada. | |||
<!-- | |||
#Apresentar código documentado de funções para: | |||
#*verificar a '''profundidade''' de uma árvore, | |||
#*contar o '''número de nós''' de uma árvore, | |||
#*contar o '''número de folhas''' de uma árvore. | |||
--> | |||
=Árvores Balanceadas= | |||
Uma '''árvore balanceada''', ou '''árvore AVL''' (AVL vem de seus criadores soviéticos Adelson Velsky e Landis), é uma árvore binária cujas profundidades das duas sub-árvores a partir de cada nó diferem no máximo em uma unidade. | |||
Caso a árvore não esteja balanceada é necessário seu '''balanceamento''' através da '''rotação simples''' ou '''rotação dupla'''. O balanceamento é requerido para as operações de inserção e remoção de elementos. | |||
Ver: <ref>Wikipédia: Árvore AVL http://pt.wikipedia.org/wiki/%C3%81rvore_AVL</ref> e <ref>Wikilivros: Árvore AVL http://pt.wikibooks.org/wiki/Algoritmos_e_Estruturas_de_Dados/%C3%81rvores_AVL</ref>. | |||
==Referências== | ==Referências== | ||
Edição atual tal como às 20h03min de 28 de novembro de 2014
Árvores
Uma árvore binária é uma estrutura de dados formada por um conjunto finito de elementos ou nós. Uma árvore pode estar vazia ou pode ser formada por um nó chamado raiz e dois sub-conjuntos de elementos chamados sub-árvore esquerda e sub-árvore direita. As sub-árvores esquerda e direita são também árvores binárias e podem estar vazias [1].
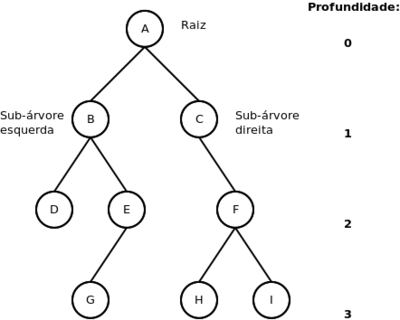
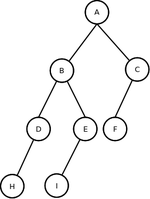
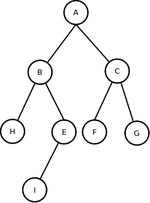
A figura abaixo ilustra uma árvore binária [1]:
Na figura:
- O nó raiz A tem duas sub-árvores B e C;
- O nó B tem duas sub-árvores D e E;
- O nó C tem apenas a sub-árvore da direita F;
- O nó E tem apenas a sub-árvore da esquerda G;
- O nó F tem duas sub-árvores H e I;
- Os nós D, G, H e I não tem sub-árvores, portanto, são chamados folhas.
Se A tem duas sub-árvores B e C, diz-se que:
- A é pai de B e C;
- B é filho esquerdo de A;
- C é filho direito de A.
- B é irmão de C.
- Profundidade da árvore binária
- Numa árvore binária, o nó raiz é considerado como profundidade 0 (zero). As sub-árvores do nó raiz profundidade 1, e assim sucessivamente. No exemplo da figura, a árvore binária tem profundidade 3.
- Árvore estritamente binária
- Uma árvore é estritamente binária se todo nó que não for folha tenha as sub-árvores direita e esquerda não vazias.
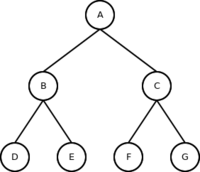
- Árvore binária completa
- Uma árvore é binária completa se for uma árvore estritamente binária e todas as folhas estiverem na mesma profundidade.
Exemplo de aplicação das árvores binárias
As árvores binárias são uma estrutura de dados útil quando precisam ser tomadas decisões bi-direcionais em cada ponto do processo. Por exemplo, suponha que queiramos encontrar repetições em uma lista de números. Uma maneira de fazer isto é comparar cada número com todos os que o precedem. Entretanto, isto pode envolver muitas comparações. Outra maneira é utilizar uma árvore binária [1].
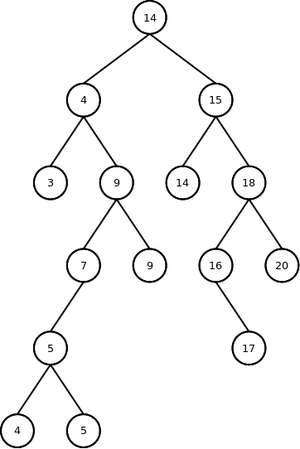
Suponha que temos a seguinte lista de números para verificar repetições:
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
Neste caso, iniciamos a árvore com o primeiro número da lista como sendo o nó raiz. Na sequência, comparamos o próximo número com o número da raiz, se for igual é uma repetição. Se for menor, comparamos com a sub-árvore da esquerda. Se for maior, comparamos com a sub-árvore da direita. Se a sub-árvore estiver vazia, incluímos o número como filho desta sub-árvore, a esquerda ou direita, caso seja menor ou maior que o conteúdo do nó, respectivamente.
Veja a árvore que seria construída neste exemplo:
Percorrendo uma árvore
Uma operação importante em uma árvore binária é percorrer todos os seus nós.
Diferentemente de uma lista, na qual os nós são percorridos de maneira linear, numa árvore, existem diferentes ordens para poder percorrê-la.
Todos os métodos para percorrer uma árvore são definidos recursivamente, de modo que percorrer uma árvore envolve visitar a raiz e depois a sub-árvore direita e a esquerda. O que difere cada método é a ordem em que estas operações são realizadas [1].
Três métodos são conhecidos para percorrer uma árvore binária:
- Em ordem, ou esquerda-raiz-direita;
- Pré-ordem ou percurso em profundidade ou raiz-esquerda-direita;
- Pós-ordem ou esquerda-direita-raiz.
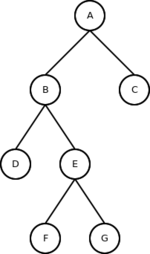
Por exemplo, dada a árvore:
A
/ \
B C
/ / \
D E F
/ \ \
G H I
- Percorrer a árvore em ordem
- Percorre-se primeiro a sub-árvore esquerda, na ordem esquerda-raiz-direita. Depois a raiz. E depois a sub-árvore direita, também na ordem esquerda-raiz-direita [2]:
4
/ \
3 7
/ / \
1 5 8
/ \ \
0 2 6
- Percorrer a árvore em pré-ordem ou em profundidade
- Percorre-se primeiro a raiz. Depois a sub-árvore esquerda, na ordem raiz-esquerda-direita. E depois a sub-árvore direita, também na ordem raiz-esquerda-direita:
0
/ \
1 5
/ / \
2 6 8
/ \ \
3 4 7
- Percorrer a árvore em pós-ordem
- Percorre-se primeiro a sub-árvore esquerda, na ordem esquerda-direita-raiz. Depois a sub-árvore direita, também na ordem esquerda-direita-raiz. E depois a raiz:
8
/ \
3 7
/ / \
2 5 6
/ \ \
0 1 4
Inserção de elementos em árvores binárias
Vários algoritmos que trabalham com árvores trabalham em duas fases. Primeiro inserem elementos na árvore e depois percorrem a árvore.
Veja um exemplo de classificação de números em ordem ascendente. A medida que os números forem sendo lidos os mesmos vão sendo inseridos na árvore. Entretanto, ao contrário do algoritmo usado para achar repetições, aqui os números repetidos também são inseridos na árvore. Quando um novo número é comparado com a raiz da árvore, a sub-árvore esquerda é utilizada para inserir se o número for menor que o conteúdo do nó e a sub-árvore direita é usada se o número for maior ou igual ao conteúdo do nó[1].
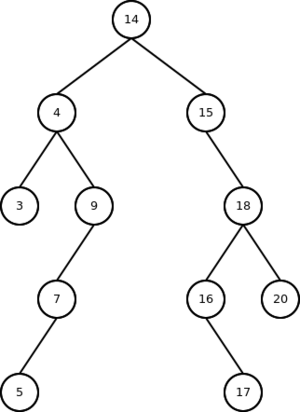
Para a lista de números
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5
a árvore resultante seria:
Note que nesta árvore, todos os elementos da esquerda do nó raiz são menores que os elementos da direita, valendo o mesmo para cada sub-árvore.
- Exercício
Percorra a árvore gerada anteriormente em ordem, ou esquerda-raiz-direita e veja a ordem dos números.
Implementação de árvores em linguagem C
Cada nó de uma árvore pode ser implementado em linguagem C como uma estrutura com três campos: um campo conteúdo, para guardar a informação deste nó, e dois campos tipo ponteiro que apontam para as sub-árvores direita e esquerda.
Os códigos abaixo foram adaptados da referência [3].
Declaração de um nó de uma árvore
typedef struct arvore {
int conteudo;
struct arvore *esq;
struct arvore *dir;
} arvore;
Note que a declaração do nó da árvore é recursiva, onde os ponteiros *esq e *dir apontam para estruturas do mesmo tipo que está sendo declarada.
Criação de uma árvore e sua definição recursiva
Uma árvore é criada a partir da declaração do endereço de sua raiz, fazendo seu ponteiro apontar para NULL, que caracteriza uma árvore vazia.
#include <stdio.h>
#include <stdlib.h>
main()
{
arvore *r = NULL; //r é um ponteiro para uma árvore vazia
...
}
Como uma árvore binária pode estar vazia ou possuir sub-árvores direita e/ou esquerda. Portanto, uma árvore binária pode ser definida de maneira recursiva, como segue:
- Um objeto r é uma árvore binária se:
- r é NULL ou
- r->esq e r->dir são árvores binárias.
Funções recursivas para percorrer uma árvore binária
- Em ordem
- Faz a varredura esquerda-raiz-direita (e-r-d):
void imprime_erd(arvore *r) {
if (r != NULL) {
imprime_erd(r->esq);
printf("%d\n", r->conteudo);
imprime_erd(r->dir);
}
}
- Pré-ordem
- Faz a varredura em profundidade ou raiz-esquerda-direita (r-e-d):
void imprime_red(arvore *r) {
if (r != NULL) {
printf("%d\n", r->conteudo);
imprime_red(r->esq);
imprime_red(r->dir);
}
}
- Pós-ordem
- Faz a varredura esquerda-direita-raiz (e-d-r):
void imprime_edr(arvore *r) {
if (r != NULL) {
imprime_edr(r->esq);
imprime_edr(r->dir);
printf("%d\n", r->conteudo);
}
}
Função recursiva para inserção em árvores binárias
Esta função recursiva insere na árvore binária à esquerda se o número for menor que a raiz ou à direita se maior ou igual:
void inserir(arvore **r, int num){
if(*r == NULL){
*r = (arvore *) malloc(sizeof(arvore));
(*r)->esq = NULL;
(*r)->dir = NULL;
(*r)->conteudo = num;
}else{
if(num < (*r)->conteudo)
inserir(&(*r)->esq, num);
else
inserir(&(*r)->dir, num);
}
}
Alguns conceitos:
- Ponteiro
- Um ponteiro aponta para um endereço de memória.
- Se ponteiro=NULL ele aponta para nada.
- Quando uma árvore binária é criada o ponteiro aponta para nada:
arvore *r=NULL;
- Quando vou inserir um elemento em uma árvore:
- Um nó é criado:
*r = (arvore *) malloc(sizeof(arvore));
- O conteúdo do ponteiro (*r) recebe endereço do novo nó criado.
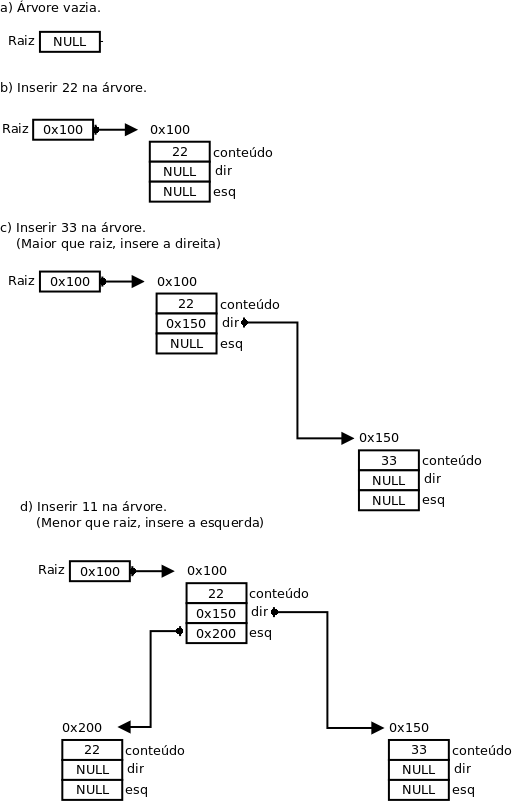
- Exemplo ilustrativo
- A figura apresenta uma sequência de operações, na qual uma árvore binária é primeiramente criada e em seguida são inseridos os números 22, 33 e 11, nesta ordem. Os endereços de memória da figura são apenas ilustrativos.
Remoção de nós de uma árvore
Numa árvore binária todos os elementos à esquerda do nó raiz são menores que os elementos à direita, valendo o mesmo para cada sub-árvore. Assim, se um nó for removido, esta característica da árvore binária deve ser respeitada.
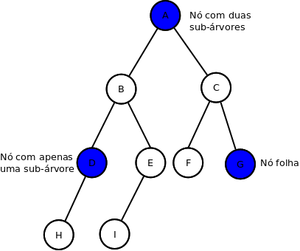
Algumas regras para remover nós de uma árvore binária:
- Se o nó é uma folha, isto é, não tem sub-árvores, o mesmo pode ser removido sem problemas. Em seguida deve-se fazer o ponteiro de seu pai apontar para NULL.
- Caso do nó G da figura.
- Se o nó tem somente uma sub-árvore (direita ou esquerda), podemos eliminar o nó "puxar" o nó filho para seu lugar.
- Caso do nó D da figura.
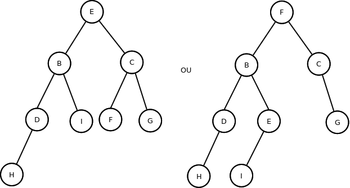
- Se o nó tem as duas sub-árvores há duas possibilidades: podemos "puxar" para seu lugar o maior elemento da sub-árvore esquerda ou o menor elemento da sub-árvore direita
- Caso do nó A da figura, podemos substitui-lo pelo maior elemento da sub-árvore esquerda, no caso o nó E, ou pelo menor elemento da sub-árvore direita, no caso o nó F.
Veja função para remover nós em [3], além de funções para verificar a profundidade de uma árvore, contar o número de nós e contar o número de folhas.
Exercícios
- Compile e teste as funções para declarar, criar, inserir e fazer a varredura dos nós de uma árvore binária.
- Construa um programa que utilize árvores binárias para encontrar repetições em uma lista de números, como no exemplo visto anteriormente.
- Construa um programa que utilize árvores binárias para ordenamento ascendente de uma sequência de números, como no exemplo visto anteriormente.
- Modifique o programa para fazer o ordenamento descendente de uma sequência de números.
- Implemente função para remover elementos de uma árvore, considerando que não há elementos duplicados.
- Implemente funções para:
- verificar a profundidade de uma árvore,
- contar o número de nós de uma árvore,
- contar o número de folhas de uma árvore.
Problema
Considere um sistema de votação por telefone, no qual cada número pode votar apenas uma vez. Considere ainda que o sistema vai armazenar os números de telefones que já votaram em uma estrutura de dados tipo árvore binária visando facilitar a busca para verificar se um dado número já votou.
- Suponha de num dado momento 1 milhão de votos já tenham sido realizados. Responda quantos nós tenho que visitar, no máximo, para saber se o número de uma nova ligação já votou ou não?
Trabalho
- Apresentar código documentado com conjunto de funções para trabalhar com árovores binárias, incluindo funções para inserir e fazer a varredura e remover dos nós de uma árvore binária.
- Utilize as funções para árvores binárias em programas que realizem as seguintes operações:
- Ordenar uma lista de 100 números inteiros;
- Ler uma lista de 100 números inteiros de um arquivo e imprimir em outro arquivo a lista dos números ordenada;
- Ler uma lista de 100 números inteiros de um arquivo e inserir em uma árvore binária. Em seguida, solicitar ao usuário a inserção ou remoção de números na árvore. No caso de inserção o programa deve verificar se o número já está na árvore e incluí-lo se não estiver. No caso de remoção o programa deve verificar se o número está na árvore antes de removê-lo. Ao fim, imprimir em arquivo a lista de números ordenada.
Árvores Balanceadas
Uma árvore balanceada, ou árvore AVL (AVL vem de seus criadores soviéticos Adelson Velsky e Landis), é uma árvore binária cujas profundidades das duas sub-árvores a partir de cada nó diferem no máximo em uma unidade.
Caso a árvore não esteja balanceada é necessário seu balanceamento através da rotação simples ou rotação dupla. O balanceamento é requerido para as operações de inserção e remoção de elementos.
Referências
- ↑ 1,0 1,1 1,2 1,3 1,4 TENENBAUM, Aaron M.; LANGSAM, Yedidyah; AUGENSTEIN, Moshe. Estruturas de dados usando C. Árvores, p. 323, Makron Books, 1995.
- ↑ FEOFILOFF, P. IME-USP, 2013. http://www.ime.usp.br/~pf/algoritmos/aulas/bint.html.
- ↑ 3,0 3,1 WIKILIVROS: Programar em C / Árvores Binárias http://pt.wikibooks.org/wiki/Programar_em_C/%C3%81rvores_bin%C3%A1rias
- ↑ Wikipédia: Árvore AVL http://pt.wikipedia.org/wiki/%C3%81rvore_AVL
- ↑ Wikilivros: Árvore AVL http://pt.wikibooks.org/wiki/Algoritmos_e_Estruturas_de_Dados/%C3%81rvores_AVL
--Evandro.cantu (discussão) 09h43min de 11 de novembro de 2014 (BRST)