Portfólio: ManoWeb: mudanças entre as edições
| (62 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 19: | Linha 19: | ||
===Introdução=== | ===Introdução=== | ||
ATRITO ENTRE SÓLIDOS | ATRITO ENTRE SÓLIDOS <ref> DOCA, Ricardo Helou; GUALTER, José Biscuola; VILLAS BÔAS, Newton - Física Volume 1, 1ª ed, editora Saraiva - 2010 </ref> | ||
O atrito é um fenômeno de grande importância em nossa vida diária. Se por um lado apresenta caráter útil e essencial em diversas situações do cotidiano, por outro revela aspectos indesejáveis. | O atrito é um fenômeno de grande importância em nossa vida diária. Se por um lado apresenta caráter útil e essencial em diversas situações do cotidiano, por outro revela aspectos indesejáveis. | ||
Se não fosse o atrito seria impossível caminhar em uma rua, bem como impraticável o movimento de um carro convencional sobre o asfalto. Na ausência do atrito, um colhedor de cocos não conseguiria subir no caule de um coqueiro para apanhar os frutos, uma lixa não desgastaria um pedaço de madeira e não poderíamos desfrutar do som emitido por um violino, já que este é obtido pelo esfregar das fibras ou dos fios do arco sobre as cordas do instrumento. Também não poderíamos escrever com um lápis sobre uma folha de papel ou sequer conseguiríamos empunhá-lo. | Se não fosse o atrito seria impossível caminhar em uma rua, bem como impraticável o movimento de um carro convencional sobre o asfalto. Na ausência do atrito, um colhedor de cocos não conseguiria subir no caule de um coqueiro para apanhar os frutos, uma lixa não desgastaria um pedaço de madeira e não poderíamos desfrutar do som emitido por um violino, já que este é obtido pelo esfregar das fibras ou dos fios do arco sobre as cordas do instrumento. Também não poderíamos escrever com um lápis sobre uma folha de papel ou sequer conseguiríamos empunhá-lo. | ||
O atrito ainda se manifesta em diversas situações do dia a dia como agente dissipador de energia, como é o caso da energia cinética( de movimento). Se, por exemplo, você lançar o apagador do quadro de giz para que ele deslize sobre o chão da sala de aula, notará que, pela ação do atrito, ele será freado e perderá a energia cinética recebida no ato de lançamento. | O atrito ainda se manifesta em diversas situações do dia a dia como agente dissipador de energia, como é o caso da energia cinética( de movimento). Se, por exemplo, você lançar o apagador do quadro de giz para que ele deslize sobre o chão da sala de aula, notará que, pela ação do atrito, ele será freado e perderá a energia cinética recebida no ato de lançamento. | ||
Consideremos dois corpos em contato comprimindo-se mutuamente. Quando um deles escorrega ou tende a escorregar em relação ao outro, há uma troca de forças, denominadas de forças de atrito. Essas forças, que sempre surgem no sentido de se opor ao escorregamento ou à tendência de escorregamento são devidas a interações de origem eletromagnética entre os átomos das regiões de contato efetivo entre as duas superfícies. | Consideremos dois corpos em contato comprimindo-se mutuamente. Quando um deles escorrega ou tende a escorregar em relação ao outro, há uma troca de forças, denominadas de forças de atrito. Essas forças, que sempre surgem no sentido de se opor ao escorregamento ou à tendência de escorregamento são devidas a interações de origem eletromagnética entre os átomos das regiões de contato efetivo entre as duas superfícies. | ||
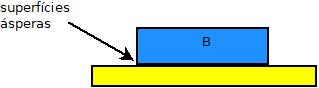
Consideremos, por exemplo, a situação abaixo em que o bloco B repousa sobre a superfície S, plana e horizontal. | Consideremos, por exemplo, a situação abaixo em que o bloco B repousa sobre a superfície S, plana e horizontal. | ||
[[Arquivo:Diagrama1.jpg]] | |||
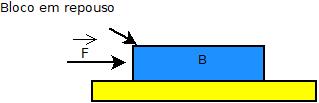
Admitamos que B seja empurrado horizontalmente para a direita por uma força <math> \vec F \</math>, mas sem sair do lugar. | |||
[[Arquivo:Diagrama2.jpg]] | |||
Ao ser empurrado, B aplica em S uma força <math> \vec F \</math> horizontal dirigida para a direita. | |||
Como se explica, então, o repouso de B? Ocorre que esse bloco recebe de S, na região de contato, uma força <math> \vec F _S\ _B</math>) horizontal dirigida para a esquerda, que equilibra a força <math> \vec F \</math>. | |||
As forças <math> \vec F _B\ _S</math> e <math> \vec F _S\ _B</math> que B e S trocam na região de contato são forças de atrito e constituem um par ação-reação (3ª lei de Newton). | |||
Observemos que <math> \vec F _B\ _S</math> e <math> \vec F _S\ _B</math> têm mesma intensidade, mesma direção e sentidos opostos, estando aplicadas em corpos diferentes. | |||
Destaquemos, ainda, que as forças de atrito <math> \vec F _B\ _S</math> e <math> \vec F _S\ _B</math> só aparecem se <math> \vec F \</math> <math> \ne</math> <math> \vec 0 \</math>.De fato, se não houver solicitação de escorregamento, não haverá troca de forças de atrito entre as superfícies em contato. Então, para o bloco B em repouso sobre a superfície S, temos: | |||
Se <math> \vec F \</math>=<math> \vec 0 \</math> <math> \Rightarrow </math> <math> \vec F _B\ _S</math>=<math> \vec F \</math>=<math> \vec 0 \</math> | |||
No caso de B já estar escorregando sobre a superfície S, as forças de atrito também estarão presentes, independentemente de <math> \vec F \</math> estar atuando ou não. | |||
===Atrito Estático=== | |||
Conceito | |||
Considere uma mesa horizontal sobre a qual repousa uma régua de madeira. Imagine uma borracha escolar apoiada sobre a face mais larga da régua. Inicialmente a borracha não recebe força de atrito, uma vez que não manifesta nenhuma tendência de escorregamento. | |||
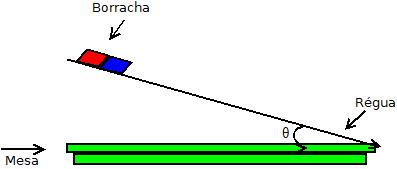
Suponha agora que a régua seja inclinada lentamente em relação a superfície da mesa, conforme sugere a figura a seguir. | |||
[[Arquivo:atrito estáticomanoweb.jpg]]. | |||
No início, para pequenos valores do ângulo <math>\theta </math>, a borracha permanece parada e a força de atrito que a mantém em equilíbrio é do tipo estático. Tal força tem intensidade crescente a partir de zero, constituindo-se na equilibrante da força que solicita a borracha a descer (componente do peso da borracha). | |||
[[Arquivo:atrito estático manoweb.jpg]] | |||
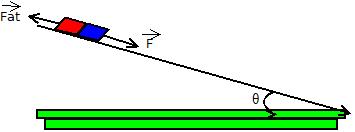
continuando a inclinar a régua de modo que aumente o ângulo <math>\theta </math>, chega-se a um ponto em que a borracha se apresenta na iminência de movimento,, isto é, está preste a descer. nesse caso, a força de atrito estático que ainda mantém a borracha em equilíbrio terá atingido a sua máxima intensidade. Essa máxima força de atrito que se manifesta quando o escorregamento é iminente, é denominada força de atrito máximo (<math> \vec F \ </math><math>_e\ _s\ _t\ _M\ _á\ _x</math>). | |||
Resumindo, vimos que a força de atrito estático tem intensidade variável desde zero, quando não há solicitação de escorregamento, até um valor máximo, quando o corpo fica na iminência de escorregar. | |||
Assim podemos dizer que: | |||
0 <math> \le </math> F<math>_a\ _t</math> <math> \le </math> F<math>_e\ _s\ _t\ _M\ _á\ _x</math> | |||
A intensidade da força de atrito estático depende da intensidade da força que visa provocar o escorregamento, sendo sempre igual à desta última. | |||
===ATRITO CINÉTICO=== | |||
Conceito | Conceito | ||
Suponha | Admita que o bloco da figura a seguir esteja em repouso sobre um plano horizontal real. Suponha que sobre ele seja aplicada uma força <math> \vec F \ </math>, paralela ao plano de apoio. com atuação de <math> \vec F \ </math>, o bloco recebe do plano a força de atrito <math> \vec F _a\ _t</math>. | ||
[[Arquivo:atritocinético.png]] | |||
Qual a condição a ser satisfeita para que o bloco seja colocado em movimento? A resposta é simples, o movimento será iniciado se a intensidade de <math> \vec F </math> superar a intensidade da <math> \vec F \ _e\ _s\ _t\ _M\ _á\ _x</math>. | |||
Supondo que esta condição tenha sido cumprida, observemos uma situação dinâmica, com o bloco em movimento. Enquanto o bloco estava em repouso, o atrito era chamado de estático. Agora, porém, receberá a denominação de '''cinético''' ou '''dinâmico''' | |||
===Coeficiente de atrito estático máximo=== | |||
Vamos considerar agora uma caixa de papelão, sem tampa e apoiada sobre a superfície plana e horizontal de um piso de concreto. Empurrando-se a caixa, inicialmente vazia, ela será colocada "facilmente" em movimento. Se colocarmos, porém, certa quantidade de areia dentro dela, a força inicial necessária para iniciar o movimento será, certamente, mais intensa que aquela aplicada no caso anterior. Se aumentarmos gradativamente a quantidade de areia dentro da caixa, notaremos que, quanto mais areia introduzirmos, maior será a intensidade da força horizontal a ser aplicada para que o movimento seja iniciado. Isso mostra que, à medida que se preenche a caixa com areia, maior se torna a força de atrito estático máximo entre a caixa e o plano horizontal. | |||
figura | |||
Assim, podemos concluir que a intensidade da força de atrito estático máximo (<math> \vec F \ _e\ _s\ _t\ _M\ _á\ _x</math>) é diretamente proporcional à intensidade da força normal (<math> \vec F \ _N</math>) trocada pelas superfícies atritantes na região de contato. | |||
Matematicamente: <math> \vec F \ _e\ _s\ _t\ _M\ _á\ _x</math>=<math>\mu\ _e \vec F \ _N</math>. | |||
A constante de proporcionalidade <math>\mu\ _e</math>, denomina-se '''coeficiente de atrito estático''', e seu valor depende dos materiais atritantes e do grau de polimento deles. | |||
==lançamento oblíquo== | |||
[[Mídia:tiro de canhão Manoel2.sb]] | |||
==Coeficiente de atrito cinético== | |||
===Procedimentos=== | |||
Considere uma mesa horizontal e sobre a mesma um arranjo de madeira que simula o plano inclinado. Nesse plano está uma massa de madeira apoiada em uma das extremidades do plano. Ao iniciar a inclinação do referido plano em relação a mesa de forma que haja variação do ângulo <math> \theta, até que o coeficiente de atrito estático máximo seja obtido e é nesse ponto em que a massa de madeira começa a deslizar sobre o plano. A partir desse movimento, o atrito que era estático passa a ser cinético, a massa adquire aceleração e velocidade constante. | |||
===Conclusão=== | |||
Com base nos dados deste experimento foi possível verificar que o coeficiente de atrito depende diretamente das superfícies que interagem. O ângulo de inclinação do plano influencia diretamente no resultado do experimento, devido ao coeficiente de atrito estático máximo depender da altura do plano, que neste caso é um dos catetos do triângulo retângulo formado pelo plano inclinado, quanto maior o ângulo, menor será o coeficiente de atrito estático e a força de atrito que irá atuar no sistema será menor, pois a tendência do movimento é contrário a esta força. | |||
Foi possível observar também que devido ao material usado, por exemplo, a régua, a mesma não possibilita uma leitura precisa do experimento com isso aumentando a incerteza das medidas dos ângulos, que irão atuar diretamente no coeficiente estático máximo | |||
==Programação scratch== | |||
[[ | [[Mídia:poligonos-manoweb.sb]] | ||
==Referências== | ==Referências== | ||
Edição atual tal como às 23h22min de 13 de novembro de 2018
Portfólio: ManoWeb
- Curso
- Licenciatura em Física
- Disciplina
- Informática Aplicada ao Ensino de Física
- Professor
- Evandro Cantú
- Equipe
- Aluno Manoel Eduardo Gomes Silva
- Aluno Webert Silva de Araujo
Tempo de Reação Humana
Gráficos com planilhas de cálculos
Experimento:Coeficiente de Atrito
Introdução
ATRITO ENTRE SÓLIDOS [1]
O atrito é um fenômeno de grande importância em nossa vida diária. Se por um lado apresenta caráter útil e essencial em diversas situações do cotidiano, por outro revela aspectos indesejáveis.
Se não fosse o atrito seria impossível caminhar em uma rua, bem como impraticável o movimento de um carro convencional sobre o asfalto. Na ausência do atrito, um colhedor de cocos não conseguiria subir no caule de um coqueiro para apanhar os frutos, uma lixa não desgastaria um pedaço de madeira e não poderíamos desfrutar do som emitido por um violino, já que este é obtido pelo esfregar das fibras ou dos fios do arco sobre as cordas do instrumento. Também não poderíamos escrever com um lápis sobre uma folha de papel ou sequer conseguiríamos empunhá-lo.
O atrito ainda se manifesta em diversas situações do dia a dia como agente dissipador de energia, como é o caso da energia cinética( de movimento). Se, por exemplo, você lançar o apagador do quadro de giz para que ele deslize sobre o chão da sala de aula, notará que, pela ação do atrito, ele será freado e perderá a energia cinética recebida no ato de lançamento.
Consideremos dois corpos em contato comprimindo-se mutuamente. Quando um deles escorrega ou tende a escorregar em relação ao outro, há uma troca de forças, denominadas de forças de atrito. Essas forças, que sempre surgem no sentido de se opor ao escorregamento ou à tendência de escorregamento são devidas a interações de origem eletromagnética entre os átomos das regiões de contato efetivo entre as duas superfícies.
Consideremos, por exemplo, a situação abaixo em que o bloco B repousa sobre a superfície S, plana e horizontal.
Admitamos que B seja empurrado horizontalmente para a direita por uma força Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} , mas sem sair do lugar.
Ao ser empurrado, B aplica em S uma força Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} horizontal dirigida para a direita. Como se explica, então, o repouso de B? Ocorre que esse bloco recebe de S, na região de contato, uma força ) horizontal dirigida para a esquerda, que equilibra a força Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} .
As forças e que B e S trocam na região de contato são forças de atrito e constituem um par ação-reação (3ª lei de Newton).
Observemos que e têm mesma intensidade, mesma direção e sentidos opostos, estando aplicadas em corpos diferentes.
Destaquemos, ainda, que as forças de atrito e só aparecem se Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec 0 \} .De fato, se não houver solicitação de escorregamento, não haverá troca de forças de atrito entre as superfícies em contato. Então, para o bloco B em repouso sobre a superfície S, temos:
Se Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} =Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec 0 \} =Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} =Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec 0 \}
No caso de B já estar escorregando sobre a superfície S, as forças de atrito também estarão presentes, independentemente de Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \} estar atuando ou não.
Atrito Estático
Conceito
Considere uma mesa horizontal sobre a qual repousa uma régua de madeira. Imagine uma borracha escolar apoiada sobre a face mais larga da régua. Inicialmente a borracha não recebe força de atrito, uma vez que não manifesta nenhuma tendência de escorregamento.
Suponha agora que a régua seja inclinada lentamente em relação a superfície da mesa, conforme sugere a figura a seguir.
No início, para pequenos valores do ângulo , a borracha permanece parada e a força de atrito que a mantém em equilíbrio é do tipo estático. Tal força tem intensidade crescente a partir de zero, constituindo-se na equilibrante da força que solicita a borracha a descer (componente do peso da borracha).
continuando a inclinar a régua de modo que aumente o ângulo , chega-se a um ponto em que a borracha se apresenta na iminência de movimento,, isto é, está preste a descer. nesse caso, a força de atrito estático que ainda mantém a borracha em equilíbrio terá atingido a sua máxima intensidade. Essa máxima força de atrito que se manifesta quando o escorregamento é iminente, é denominada força de atrito máximo (Falhou ao verificar gramática (erro de sintaxe): {\displaystyle _e\ _s\ _t\ _M\ _á\ _x} ).
Resumindo, vimos que a força de atrito estático tem intensidade variável desde zero, quando não há solicitação de escorregamento, até um valor máximo, quando o corpo fica na iminência de escorregar.
Assim podemos dizer que:
0 F FFalhou ao verificar gramática (erro de sintaxe): {\displaystyle _e\ _s\ _t\ _M\ _á\ _x}
A intensidade da força de atrito estático depende da intensidade da força que visa provocar o escorregamento, sendo sempre igual à desta última.
ATRITO CINÉTICO
Conceito
Admita que o bloco da figura a seguir esteja em repouso sobre um plano horizontal real. Suponha que sobre ele seja aplicada uma força , paralela ao plano de apoio. com atuação de , o bloco recebe do plano a força de atrito .
Qual a condição a ser satisfeita para que o bloco seja colocado em movimento? A resposta é simples, o movimento será iniciado se a intensidade de superar a intensidade da Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \ _e\ _s\ _t\ _M\ _á\ _x}
.
Supondo que esta condição tenha sido cumprida, observemos uma situação dinâmica, com o bloco em movimento. Enquanto o bloco estava em repouso, o atrito era chamado de estático. Agora, porém, receberá a denominação de cinético ou dinâmico
Coeficiente de atrito estático máximo
Vamos considerar agora uma caixa de papelão, sem tampa e apoiada sobre a superfície plana e horizontal de um piso de concreto. Empurrando-se a caixa, inicialmente vazia, ela será colocada "facilmente" em movimento. Se colocarmos, porém, certa quantidade de areia dentro dela, a força inicial necessária para iniciar o movimento será, certamente, mais intensa que aquela aplicada no caso anterior. Se aumentarmos gradativamente a quantidade de areia dentro da caixa, notaremos que, quanto mais areia introduzirmos, maior será a intensidade da força horizontal a ser aplicada para que o movimento seja iniciado. Isso mostra que, à medida que se preenche a caixa com areia, maior se torna a força de atrito estático máximo entre a caixa e o plano horizontal.
figura
Assim, podemos concluir que a intensidade da força de atrito estático máximo (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F \ _e\ _s\ _t\ _M\ _á\ _x}
) é diretamente proporcional à intensidade da força normal () trocada pelas superfícies atritantes na região de contato.
Matematicamente: Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \vec F \ _e\ _s\ _t\ _M\ _á\ _x}
=.
A constante de proporcionalidade , denomina-se coeficiente de atrito estático, e seu valor depende dos materiais atritantes e do grau de polimento deles.
lançamento oblíquo
Mídia:tiro de canhão Manoel2.sb
Coeficiente de atrito cinético
Procedimentos
Considere uma mesa horizontal e sobre a mesma um arranjo de madeira que simula o plano inclinado. Nesse plano está uma massa de madeira apoiada em uma das extremidades do plano. Ao iniciar a inclinação do referido plano em relação a mesa de forma que haja variação do ângulo <math> \theta, até que o coeficiente de atrito estático máximo seja obtido e é nesse ponto em que a massa de madeira começa a deslizar sobre o plano. A partir desse movimento, o atrito que era estático passa a ser cinético, a massa adquire aceleração e velocidade constante.
Conclusão
Com base nos dados deste experimento foi possível verificar que o coeficiente de atrito depende diretamente das superfícies que interagem. O ângulo de inclinação do plano influencia diretamente no resultado do experimento, devido ao coeficiente de atrito estático máximo depender da altura do plano, que neste caso é um dos catetos do triângulo retângulo formado pelo plano inclinado, quanto maior o ângulo, menor será o coeficiente de atrito estático e a força de atrito que irá atuar no sistema será menor, pois a tendência do movimento é contrário a esta força. Foi possível observar também que devido ao material usado, por exemplo, a régua, a mesma não possibilita uma leitura precisa do experimento com isso aumentando a incerteza das medidas dos ângulos, que irão atuar diretamente no coeficiente estático máximo
Programação scratch
Referências
- ↑ DOCA, Ricardo Helou; GUALTER, José Biscuola; VILLAS BÔAS, Newton - Física Volume 1, 1ª ed, editora Saraiva - 2010