Scratch: Fisica e as Equacoes do Movimento: mudanças entre as edições
m (Evandro.cantu moveu Laboratorio: Programacao Scratch e Equacoes do Movimento para Scratch: Fisica e as Equacoes do Movimento) |
|||
| (23 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 26: | Linha 26: | ||
;Criando variáreis: Vamos utilizar '''variáveis''' para guardar as informações da equação movimento que vamos estudar. | ;Criando variáreis: Vamos utilizar '''variáveis''' para guardar as informações da equação movimento que vamos estudar. | ||
:Para simular a evolução do '''tempo''' ('''t'''), vamos criar uma variável chamada '''dt''' que é um '''passo pequeno de variação do tempo''' (por exemplo | :Para simular a evolução do '''tempo''' ('''t'''), vamos criar uma variável chamada '''dt''' que é um '''passo pequeno de variação do tempo''' (por exemplo: 0,05 s) para vermos a evolução dos dados da equação. | ||
;Iniciando as variáveis: Vamos definir dt = 0,05 s e v = 10 m/s, | ;Iniciando as variáveis: Vamos definir dt = 0,05 s e v = 10 m/s, | ||
| Linha 38: | Linha 38: | ||
;Construindo um programa para mostrar a evolução da equação: Vamos considerar a evolução de '''s''' em função de '''t''' até que t = 10s. | ;Construindo um programa para mostrar a evolução da equação: Vamos considerar a evolução de '''s''' em função de '''t''' até que t = 10s. | ||
repita t | repita até t > 10 | ||
mude t para t + dt | mude t para t + dt | ||
mude s para s0 + v * t | mude s para s0 + v * t | ||
| Linha 51: | Linha 51: | ||
Depois, dentro do laço de repetição, faça com que a posição x varie de acordo com a variação de s: | Depois, dentro do laço de repetição, faça com que a posição x varie de acordo com a variação de s: | ||
mude x para | mude x para -180 + s | ||
[[Mídia:MRU-movimento.sb]] | |||
====Exercícios:==== | ====Exercícios:==== | ||
| Linha 57: | Linha 59: | ||
#Mude o valor da posição inicial e veja a mudança no movimento do personagem | #Mude o valor da posição inicial e veja a mudança no movimento do personagem | ||
===Traçando | ===Traçando o gráfico do movimento=== | ||
Salve o arquivo com as equações do movimento com outro nome. | Salve o arquivo com as equações do movimento com outro nome. | ||
| Linha 81: | Linha 83: | ||
abaixe a caneta | abaixe a caneta | ||
repita t | repita até t > 10 | ||
mude t para t + dt | mude t para t + dt | ||
mude s para s0 + v * t | mude s para s0 + v * t | ||
mude x para -180 + t | mude x para -180 + t | ||
mude y para -120 + s | mude y para -120 + s | ||
:Note que | :Note que: | ||
:*No '''eixo x''' vamos representar a evolução do '''tempo''' ('''t'''); | |||
:*No '''eixo y''' a evolução da '''posição''' ('''s'''). | |||
:Ajuste a escala do gráfico, por exemplo, multiplicando a escala de tempo por 10. | :Ajuste a escala do gráfico, por exemplo, multiplicando a escala de tempo por 10. | ||
| Linha 94: | Linha 98: | ||
====Exercícios==== | ====Exercícios==== | ||
#Construa uma simulação para o '''MRUV'''. | #Construa uma simulação para o '''MRUV'''. | ||
#Construa um gráfico para a função do deslocamento no '''MRUV'''. | #Construa um gráfico para a função do deslocamento no '''MRUV''', considerando os seguintes valores: | ||
:*Aceleração constante = 1,2 m/s; | |||
:*Velocidade inicial = 4 m/s; | |||
:*Posição inicial = 8m; | |||
:*Tempo variando entre 0 e 10 s. | |||
===Lançamento oblíquo no vácuo=== | ===Lançamento oblíquo no vácuo=== | ||
| Linha 103: | Linha 111: | ||
Outro exemplo são o '''lançamento de projéteis''', também conhecido como '''movimento balístico'''. | Outro exemplo são o '''lançamento de projéteis''', também conhecido como '''movimento balístico'''. | ||
;Análise do movimento oblíquo no vácuo: Deve-se decompor a velocidade inicial (v<sub>0</sub>) em suas componentes horizontal (v<sub>0x</sub>) e vertical (v<sub>0y</sub>), em função do ângulo de lançamento & | ;Análise do movimento oblíquo no vácuo: Deve-se decompor a velocidade inicial (v<sub>0</sub>) em suas componentes horizontal (v<sub>0x</sub>) e vertical (v<sub>0y</sub>), em função do ângulo de lançamento Θ: | ||
[[Arquivo:LancamentoObliquo.jpg | 400px]] Fonte:<ref>http://osfundamentosdafisica.blogspot.com.br/2011/01/preparando-se-para-as-provas_17.html</ref>. | |||
v<sub>0x</sub> = v<sub>0</sub> . cos Θ | |||
v<sub>0y</sub> = v<sub>0</sub> . sen Θ | |||
Movimento na horizontal: | |||
s<sub>x</sub> = v<sub>0x</sub> . t | |||
Movimento na vertical: | |||
s<sub>y</sub> = v<sub>0y</sub> . t - g . t<sup>2</sup> / 2 | |||
:onde g é a aceleração da gravidade (≈ 9,8 m/s<sup>2</sup>) | |||
====Projeto de Aplicação com programação Scratch==== | |||
#Construa uma aplicação no '''Scratch''' para traçar o '''gráfico do movimento oblíquo no vácuo''', ilustrando um '''lançamento de projétil''', com possibilidade de escolha da velocidade inicial (v<sub>0</sub>) e do ângulo de lançamento (Θ). Ilustre a aplicação construindo um '''ambiente temático''' para o movimento oblíquo, como por exemplo, uma tacada de golfe, um arremesso de basquete, um lançamento de dardo, etc. | |||
==Referências== | |||
<references /> | |||
---- | ---- | ||
| Linha 118: | Linha 134: | ||
---- | ---- | ||
[[Categoria:Scratch]] | [[Categoria:Scratch]] [[Categoria:Informática Aplicada ao Ensino de Física]] | ||
Edição atual tal como às 11h48min de 27 de setembro de 2023
Laboratório: Programação Scratch e Equações do Movimento
Com a programação Scratch é possível construir um ambiente simulado para estudar as equações do movimento da física. Para tal, vamos utilizar lógica de programação para construir um programa com as estruturas de controle, variáveis e operadores lógicos e matemáticos do Scratch.
Móveis em movimento
As equações da física que permitem modelar móveis em movimento são:
- Função horária da posição em um Movimento Retilíneo Uniforme (MRU)
s = s0 + vt
- Função horária da posição e velocidade em um Movimento Retilíneo Uniforme Variado (MRUV)
s = s0 + v0t + at2 / 2 v = v0 + at
Programação Scratch e estudo dos móveis em movimento
- Mudança de personagem para acompanhar o movimento
- O gatinho é o personagem principal do ambiente Scratch, contudo, podemos substituí-lo por outro personagem, por exemplo, um fusca, para o colocarmos em movimento.
- Para tal, clique com o botão direito para apagá-lo e inclua outro personagem a partir da área de criação de Sprites.
Simulação de Movimento Retilíneo Uniforme
A função horária da posição em um Movimento Retilíneo Uniforme (MRU) é
s = s0 + vt
- Criando variáreis
- Vamos utilizar variáveis para guardar as informações da equação movimento que vamos estudar.
- Para simular a evolução do tempo (t), vamos criar uma variável chamada dt que é um passo pequeno de variação do tempo (por exemplo: 0,05 s) para vermos a evolução dos dados da equação.
- Iniciando as variáveis
- Vamos definir dt = 0,05 s e v = 10 m/s,
mude s0 para 0 mude t para 0 mude dt para 0,05 mude v para 10 mude s para s0 + v * t
- Construindo um programa para mostrar a evolução da equação
- Vamos considerar a evolução de s em função de t até que t = 10s.
repita até t > 10 mude t para t + dt mude s para s0 + v * t
Implemente as variáveis e o código no Scratch e veja a evolução das variáveis.
- Colocando o personagem em movimento
- Vamos movimentar nosso personagem de acordo com a posição s.
Para tal, após a inicialização das variáveis, posicione o personagem embaixo e a esquerda do plano cartesiano do palco.
mude x para -180 mude y para -120
Depois, dentro do laço de repetição, faça com que a posição x varie de acordo com a variação de s:
mude x para -180 + s
Exercícios:
- Mude o valor da velocidade e veja a mudança no movimento do personagem.
- Mude o valor da posição inicial e veja a mudança no movimento do personagem
Traçando o gráfico do movimento
Salve o arquivo com as equações do movimento com outro nome.
Crie um novo sprite, ou personagem, que se movimentará para traçar a equação do movimento, por exemplo, um fantasminha.
- Movimento para este novo personagem
- O novo personagem vai se movimentar no plano cartesiano xy e usar a caneta para traçar o gráfico do deslocamento pelo tempo (s x t).
A inicialização das variáveis será a mesma utilizada para simular o movimento do móvel:
mude s0 para 0 mude t para 0 mude dt para 0,05 mude v para 5 mude s para s0 + v * t
Posição inicial do personagem também pode ser a mesma:
mude x para -180 mude y para -120
- Laço de repetição
- A evolução das variáveis no laço de repetição será a mesma, apenas teremos que nos preocupar com o movimento do personagem que vai traçar o gráfico e com a caneta.
Antes de entrar no laço de repetição:
abaixe a caneta
repita até t > 10 mude t para t + dt mude s para s0 + v * t mude x para -180 + t mude y para -120 + s
- Note que:
- No eixo x vamos representar a evolução do tempo (t);
- No eixo y a evolução da posição (s).
- Ajuste a escala do gráfico, por exemplo, multiplicando a escala de tempo por 10.
Ao sair do laço de repetição:
levante a caneta
Exercícios
- Construa uma simulação para o MRUV.
- Construa um gráfico para a função do deslocamento no MRUV, considerando os seguintes valores:
- Aceleração constante = 1,2 m/s;
- Velocidade inicial = 4 m/s;
- Posição inicial = 8m;
- Tempo variando entre 0 e 10 s.
Lançamento oblíquo no vácuo
O lançamento oblíquo ocorre quando temos componente de velocidade horizontal e um componente de velocidade vertical.
Um exemplo de movimento deste tipo é uma prova de salto em distância, onde o atleta deve combinar uma boa velocidade de aproximação e um ângulo de projeção do salto, junto a tábua de impulsão.
Outro exemplo são o lançamento de projéteis, também conhecido como movimento balístico.
- Análise do movimento oblíquo no vácuo
- Deve-se decompor a velocidade inicial (v0) em suas componentes horizontal (v0x) e vertical (v0y), em função do ângulo de lançamento Θ:
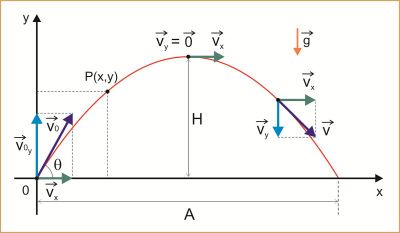 Fonte:[1].
Fonte:[1].
v0x = v0 . cos Θ v0y = v0 . sen Θ
Movimento na horizontal:
sx = v0x . t
Movimento na vertical:
sy = v0y . t - g . t2 / 2
- onde g é a aceleração da gravidade (≈ 9,8 m/s2)
Projeto de Aplicação com programação Scratch
- Construa uma aplicação no Scratch para traçar o gráfico do movimento oblíquo no vácuo, ilustrando um lançamento de projétil, com possibilidade de escolha da velocidade inicial (v0) e do ângulo de lançamento (Θ). Ilustre a aplicação construindo um ambiente temático para o movimento oblíquo, como por exemplo, uma tacada de golfe, um arremesso de basquete, um lançamento de dardo, etc.
Referências
--Evandro.cantu (discussão) 15h15min de 15 de outubro de 2014 (BRT)