Portfólio: Cris e Greg: mudanças entre as edições
| (55 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 16: | Linha 16: | ||
==Experimento:Velocidade média e velocidade instantânea== | ==Experimento:Velocidade média e velocidade instantânea== | ||
[[Arquivo:DesenhoC&G.png|300px]] | ===Objetivos=== | ||
*Analisar o movimento de uma 'esfera' ao descer o plano inclinado e calcular a velocidade média. | |||
*Elaborar procedimento para estimar a velocidade instantânea. | |||
===Material=== | |||
*Calha com inclinação variável(1,75m comprimento), esfera, cronômetro, régua | |||
===Procedimento=== | |||
*Este experimento propõe explorar os conceitos de velocidade média e velocidade instantânea. Para isso foi utilizado uma calha (plano inclinado) e uma pequena esfera (bolinha de gude), esta foi solta a partir do repouso e seu tempo foi medido, tanto para o trajeto total (velocidade média) quanto partes dele (velocidade instantânea). | |||
[[Arquivo:DesenhoC&G.png|300px]] | |||
[[Arquivo:C&G.jpg|300px]] | |||
==Tabelas de dados e gráficos== | ==Tabelas de dados e gráficos== | ||
*A partir desse experimento foram obtidos os seguintes dados. | |||
[[Mídia: | *Foi coletado um total de dez medidas de tempo | ||
===Formulas | |||
{| border="4" cellpadding="2" | |||
! Nº medida | |||
! Tempo (s) | |||
! Desvio Padrão (Δ xi)² | |||
|- | |||
| 1 || 4,60 || 0,01 | |||
|- | |||
| 2 || 4,61 || 0,0121 | |||
|- | |||
| 3 || 4,20 || 0,09 | |||
|- | |||
| 4 || 4,47 || 0,0009 | |||
|- | |||
| 5 || 4,41 || 0,0081 | |||
|- | |||
| 6 || 4,40 || 0,01 | |||
|- | |||
| 7 || 4,48 || 0,0004 | |||
|- | |||
| 8 || 4,49 || 0,0081 | |||
|- | |||
| 9 || 4,40 || 0,01 | |||
|- | |||
| 10|| 4,66 || 0,0256 | |||
|- | |||
| Tempo médio = 4,5 | |||
|} | |||
*A partir do tempo médio, acharemos a velocidade média,levando em consideração a fórmula da velocidade média e que temos, o comprimento da calha. | |||
{| border="4" cellpadding="2" | |||
! Nº medida | |||
! (Tempo ± 0,01) s | |||
! Desvio Padrão (Δ xi)² | |||
|- | |||
| 1 || 0,27 || 0,0004 | |||
|- | |||
| 2 || 0,26 || 0,0001 | |||
|- | |||
| 3 || 0,26 || 0,0001 | |||
|- | |||
| 4 || 0,20 || 0,0025 | |||
|- | |||
| 5 || 0,20 || 0,0025 | |||
|- | |||
| 6 || 0,24 || 0,0001 | |||
|- | |||
| 7 || 0,22 || 0,0009 | |||
|- | |||
| 8 || 0,23 || 0,0004 | |||
|- | |||
| 9 || 0,28 || 0,0009 | |||
|- | |||
| 10|| 0,29 || 0,0016 | |||
|- | |||
| Velocidade instantânea para um intervalo de 5 cm de deslocamento = (20,00 ± 0,05) 𝑐𝑚⁄s | |||
|} | |||
{| border="4" cellpadding="2" | |||
! Nº medida | |||
! (Tempo ± 0,00) s | |||
! Desvio Padrão (Δ xi)² | |||
|- | |||
| 1 || 0,17 || 0,0001 | |||
|- | |||
| 2 || 0,16 || 0,0000 | |||
|- | |||
| 3 || 0,15 || 0,0001 | |||
|- | |||
| 4 || 0,15 || 0,0001 | |||
|- | |||
| 5 || 0,17 || 0,0001 | |||
|- | |||
| 6 || 0,15 || 0,0001 | |||
|- | |||
| 7 || 0,15 || 0,0001 | |||
|- | |||
| 8 || 0,15 || 0,0001 | |||
|- | |||
| 9 || 0,15 || 0,0001 | |||
|- | |||
| 10|| 0,15 || 0,0001 | |||
|- | |||
| Velocidade instantânea para um intervalo de 20 cm do final da calha = (31,25 ± 0,01) 𝑐𝑚⁄s | |||
|} | |||
{| border="4" cellpadding="2" | |||
! (Deslocamento ± 0,05)cm | |||
! (Tempo ± 0,41)s | |||
|- | |||
| 0,00 || | 0,00 | |||
|- | |||
| 10,00 || | 1,12 | |||
|- | |||
| 20,00 || | 1,70 | |||
|- | |||
| 30,00 || |2,12 | |||
|- | |||
| 40,00 || |2,48 | |||
|- | |||
| 50,00 || | 2,81 | |||
|- | |||
| 60,00 || |3,11 | |||
|- | |||
| 70,00 || | 3,37 | |||
|- | |||
| 80,00 || | 3,64 | |||
|- | |||
| 90,00 || | 3,90 | |||
|- | |||
| 100,00 || | 4,14 | |||
|- | |||
| 110,00 || | 4,35 | |||
|- | |||
|} | |||
*Com os dados acima foi possível construir um gráfico da posição ocupada pela esfera ao | |||
longo do tempo. | |||
[[Mídia:grafico C&G.xlsx|Gráficos]] | |||
==Mapa conceitual== | |||
Mapa conceitual velocidade [http://200.17.101.9:8080/rid=1SY6WN6M1-X5W43Z-GKW/CRIS%26GREG.cmap] | |||
==Formulas== | |||
Função Afim | Função Afim | ||
| Linha 32: | Linha 184: | ||
s = s<sub>0</sub> + v<sub>0</sub> t + 1/2 a t<sup>2</sup> | s = s<sub>0</sub> + v<sub>0</sub> t + 1/2 a t<sup>2</sup> | ||
Velocidade média | Velocidade média | ||
<math>v_m</math>= <math>\frac{\Delta S}{\Delta t}</math>=<math>\frac{S-S0}{t-t0}</math> | <math>v_m</math>= <math>\frac{\Delta S}{\Delta t}</math>=<math>\frac{S-S0}{t-t0}</math> | ||
Média | |||
<math>X</math>= <math>\frac{\sum_T}{\ T}</math> | |||
Desvio padrão | |||
σ= √<math>\frac{\sum\Delta Xi^2}{\ T}</math> | |||
Desvio padrão da média | |||
σm=<math>\frac{\sigma}{√n}</math> | |||
==conclusões== | |||
*A precisão das medidas realizadas nesse experimentos não são lá de grande confiança, mas fornecem uma boa noção do fenômeno físico por trás do experimento. Fatores como: equipamentos inadequados, falta de habilidade para manuseio dos equipamentos, número de amostra pequena, tudo isso pode ser levado em conta na hora de atribuir os erros pertencentes as medidas. Procurou-se fazer mais do que uma medida, geralmente uma amostra de 10 medidas para poder conferir um mínimo grau de honestidade e dignidade as medições e ao experimento. | |||
==Experimento força de atrito== | |||
== Introdução == | |||
A força de contato que atua na superfície de um corpo sempre se opõe a tendência de escorregamento ou deslizamento em relação à superfície de um plano chamada força de atrito. As forças de atrito são muito importantes na vida cotidiana; provocam desgastes nas peças móveis das máquinas e são responsáveis pelo aumento da energia interna das mesmas, porque as peças aquecem. Por outro lado, sem atrito não haveria transmissão do movimento por correias, não poderíamos caminhar, nem escrever e até mesmo uma corrente de ar poderia fazer com que os móveis se movessem. | |||
===Objetivos=== | |||
O objetivo do trabalho era descobrir a força de atrito estático máxima. | |||
===Materiais=== | |||
Plano inclinado, régua, transferidor, bloco, calculadora | |||
[[Arquivo:Bloco.jpg|300px]] | |||
[[Arquivo:Ângulo.jpg|300px]] | |||
===Procedimentos e resultados=== | |||
Para a realização deste trabalho, utilizamos um plano inclinado com um bloco em cima e precisávamos descobrir sua força de atrito estático máxima. Para isto, usamos o transferidor para medir o ângulo necessário para o inicio do movimento do bloco, medimos 10 vezes para obter um resultado mais confiável. | |||
''TABELA DE DADOS:'' | |||
{| class="wikitable" | |||
|- | |||
| Número de análise || Ângulo | |||
|- | |||
| 01 || 30° | |||
|- | |||
| 02 || 31° | |||
|- | |||
| 03 || 29° | |||
|- | |||
| 04 || 29° | |||
|- | |||
| 05 || 30° | |||
|- | |||
| 06 || 30° | |||
|- | |||
| 07 || 29° | |||
|- | |||
| 08 || 31° | |||
|- | |||
| 09 || 30° | |||
|- | |||
| 10 || 29° | |||
|} | |||
Após a coleta de dados, foi feito o cálculo de desvio padrão e desvio padrão da média e o resultado obtido foi igual a: | |||
θ=(29,80 ± 0,25) | |||
Sabendo que: | |||
Fe=Px | |||
Px=Psen∝ | |||
N=Py | |||
Py=Pcos∝ | |||
Teremos que: | |||
Fe<sub>máx</sub>=Psen∝ | |||
N.μ=Psen∝ | |||
μ=Psen∝/N | |||
μ=Psen∝/Pcos∝ | |||
μ=Tg∝ | |||
Com isto, podemos utilizar o resultado obtido anteriormente para descobrir o coeficiente de atrito estático, que será: | |||
μ=(0,57 ± 0,0044) | |||
μ=(0,570 ± 0,004) | |||
---- | |||
[[Categoria:Portfólio Licenciatura]] | |||
==Programação Scratch== | |||
[[Mídia:Scratch Pronto.sb|Scratch]] | |||
===Lançamento obliquo== | |||
[[Mídia:LANÇAMENTO OBLIQUO C&G.sb|scratch]] | |||
==Referências== | ==Referências== | ||
| Linha 42: | Linha 280: | ||
---- | ---- | ||
Edição atual tal como às 23h05min de 13 de novembro de 2018
Portfólio: Cris e Greg
- Curso
- Licenciatura em Física
- Disciplina
- Informática Aplicada ao Ensino de Física
- Professor
- Evandro Cantú
- Equipe
- Anthony Gattelli
- Rafael Vieira
Experimento: Tempo de reação humana
O experimento teve como objetivo medir o tempo de ração humana através da queda de uma régua.
Gráficos
Experimento:Velocidade média e velocidade instantânea
Objetivos
- Analisar o movimento de uma 'esfera' ao descer o plano inclinado e calcular a velocidade média.
- Elaborar procedimento para estimar a velocidade instantânea.
Material
- Calha com inclinação variável(1,75m comprimento), esfera, cronômetro, régua
Procedimento
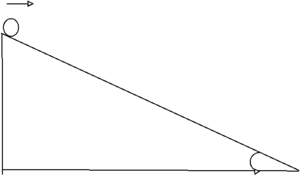
- Este experimento propõe explorar os conceitos de velocidade média e velocidade instantânea. Para isso foi utilizado uma calha (plano inclinado) e uma pequena esfera (bolinha de gude), esta foi solta a partir do repouso e seu tempo foi medido, tanto para o trajeto total (velocidade média) quanto partes dele (velocidade instantânea).

Tabelas de dados e gráficos
- A partir desse experimento foram obtidos os seguintes dados.
- Foi coletado um total de dez medidas de tempo
| Nº medida | Tempo (s) | Desvio Padrão (Δ xi)² |
|---|---|---|
| 1 | 4,60 | 0,01 |
| 2 | 4,61 | 0,0121 |
| 3 | 4,20 | 0,09 |
| 4 | 4,47 | 0,0009 |
| 5 | 4,41 | 0,0081 |
| 6 | 4,40 | 0,01 |
| 7 | 4,48 | 0,0004 |
| 8 | 4,49 | 0,0081 |
| 9 | 4,40 | 0,01 |
| 10 | 4,66 | 0,0256 |
| Tempo médio = 4,5 |
- A partir do tempo médio, acharemos a velocidade média,levando em consideração a fórmula da velocidade média e que temos, o comprimento da calha.
| Nº medida | (Tempo ± 0,01) s | Desvio Padrão (Δ xi)² |
|---|---|---|
| 1 | 0,27 | 0,0004 |
| 2 | 0,26 | 0,0001 |
| 3 | 0,26 | 0,0001 |
| 4 | 0,20 | 0,0025 |
| 5 | 0,20 | 0,0025 |
| 6 | 0,24 | 0,0001 |
| 7 | 0,22 | 0,0009 |
| 8 | 0,23 | 0,0004 |
| 9 | 0,28 | 0,0009 |
| 10 | 0,29 | 0,0016 |
| Velocidade instantânea para um intervalo de 5 cm de deslocamento = (20,00 ± 0,05) 𝑐𝑚⁄s |
| Nº medida | (Tempo ± 0,00) s | Desvio Padrão (Δ xi)² |
|---|---|---|
| 1 | 0,17 | 0,0001 |
| 2 | 0,16 | 0,0000 |
| 3 | 0,15 | 0,0001 |
| 4 | 0,15 | 0,0001 |
| 5 | 0,17 | 0,0001 |
| 6 | 0,15 | 0,0001 |
| 7 | 0,15 | 0,0001 |
| 8 | 0,15 | 0,0001 |
| 9 | 0,15 | 0,0001 |
| 10 | 0,15 | 0,0001 |
| Velocidade instantânea para um intervalo de 20 cm do final da calha = (31,25 ± 0,01) 𝑐𝑚⁄s |
| (Deslocamento ± 0,05)cm | (Tempo ± 0,41)s |
|---|---|
| 0,00 | 0,00 |
| 10,00 | 1,12 |
| 20,00 | 1,70 |
| 30,00 | 2,12 |
| 40,00 | 2,48 |
| 50,00 | 2,81 |
| 60,00 | 3,11 |
| 70,00 | 3,37 |
| 80,00 | 3,64 |
| 90,00 | 3,90 |
| 100,00 | 4,14 |
| 110,00 | 4,35 |
- Com os dados acima foi possível construir um gráfico da posição ocupada pela esfera ao
longo do tempo.
Mapa conceitual
Mapa conceitual velocidade [1]
Formulas
Função Afim
y = ax + b
Equação horária da posição
s = s0 + v0 t + 1/2 a t2
Velocidade média
= =
Média
=
Desvio padrão
σ= √
Desvio padrão da média
σm=Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{\sigma}{√n}}
conclusões
- A precisão das medidas realizadas nesse experimentos não são lá de grande confiança, mas fornecem uma boa noção do fenômeno físico por trás do experimento. Fatores como: equipamentos inadequados, falta de habilidade para manuseio dos equipamentos, número de amostra pequena, tudo isso pode ser levado em conta na hora de atribuir os erros pertencentes as medidas. Procurou-se fazer mais do que uma medida, geralmente uma amostra de 10 medidas para poder conferir um mínimo grau de honestidade e dignidade as medições e ao experimento.
Experimento força de atrito
Introdução
A força de contato que atua na superfície de um corpo sempre se opõe a tendência de escorregamento ou deslizamento em relação à superfície de um plano chamada força de atrito. As forças de atrito são muito importantes na vida cotidiana; provocam desgastes nas peças móveis das máquinas e são responsáveis pelo aumento da energia interna das mesmas, porque as peças aquecem. Por outro lado, sem atrito não haveria transmissão do movimento por correias, não poderíamos caminhar, nem escrever e até mesmo uma corrente de ar poderia fazer com que os móveis se movessem.
Objetivos
O objetivo do trabalho era descobrir a força de atrito estático máxima.
Materiais
Plano inclinado, régua, transferidor, bloco, calculadora
Procedimentos e resultados
Para a realização deste trabalho, utilizamos um plano inclinado com um bloco em cima e precisávamos descobrir sua força de atrito estático máxima. Para isto, usamos o transferidor para medir o ângulo necessário para o inicio do movimento do bloco, medimos 10 vezes para obter um resultado mais confiável.
TABELA DE DADOS:
| Número de análise | Ângulo |
| 01 | 30° |
| 02 | 31° |
| 03 | 29° |
| 04 | 29° |
| 05 | 30° |
| 06 | 30° |
| 07 | 29° |
| 08 | 31° |
| 09 | 30° |
| 10 | 29° |
Após a coleta de dados, foi feito o cálculo de desvio padrão e desvio padrão da média e o resultado obtido foi igual a:
θ=(29,80 ± 0,25)
Sabendo que:
Fe=Px Px=Psen∝ N=Py Py=Pcos∝
Teremos que:
Femáx=Psen∝ N.μ=Psen∝ μ=Psen∝/N μ=Psen∝/Pcos∝ μ=Tg∝
Com isto, podemos utilizar o resultado obtido anteriormente para descobrir o coeficiente de atrito estático, que será:
μ=(0,57 ± 0,0044) μ=(0,570 ± 0,004)
Programação Scratch
=Lançamento obliquo
Referências







